信号与系统课程实验项目教学装置

实验项目

1、基本运算单元实验

2、阶跃响应与冲激响应实验

3、连续时间系统的模拟实验

4、有源、无源滤波器实验

5、抽样定理与信号恢复实验

6、二阶网络状态轨迹的显示实验

7、一阶电路的暂态响应实验

8、二阶电路的暂态响应实验

9、二阶电路传输特性实验

10、二阶网络函数的模拟实验

10、矩形脉冲信号的分解实验

11、矩形脉冲信号的合成实验

12、谐波幅度对波形合成的影响实验

信号与系统实验指导书 实验一 零输入响应零状态响应

一、实验目的

1、掌握电路的零输入响应。

2、掌握电路的零状态响应。

3、学会电路的零状态响应与零输入响应的观察方法。

二、实验内容

1、观察零输入响应的过程。

2、观察零状态响应的过程。

三、实验仪器

1、信号与系统实验箱一台（主板）。

2、系统时域与频域分析模块一块。

3、20MHz示波器一台。

四、实验原理

1、零输入响应与零状态响应：

零输入响应：没有外加激励的作用，只有起始状态（起始时刻系统储能）所产生的响应。

零状态响应：不考虑起始时刻系统储能的作用（起始状态等于零）。

2、典型电路分析：

电路的响应一般可分解为零输入响应和零状态响应。首先考察一个实例：在下图中由RC组成一电路，电容两端有起始电压Vc(0-),激励源为e(t)。

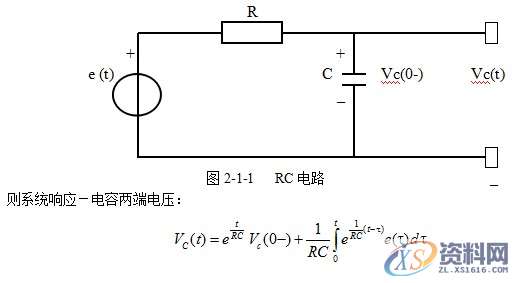
上式中第一项称之为零输入响应，与输入激励无关，零输入响应是以初始电压值开始，以指数规律进行衰减。

第二项与起始储能无关，只与输入激励有关，被称为零状态响应。在不同的输入信号下，电路会表征出不同的响应。

五、实验步骤

1、把系统时域与频域分析模块插在主板上，用导线接通此模块“电源接入”和主板上的电源（看清标识，防止接错，带保护电路），并打开此模块的电源开关。

2、系统的零输入响应特性观察

（1）接通主板上的电源，同时按下此模块上两个电源开关，将“时域抽样定理”模块中的抽样脉冲信号（SK1000用于选择频段，“频率调节”用于在频段内的频率调节，“脉宽调节”用于脉冲宽度的调节，以下实验都可改变以上的参数进行相关的操作），通过导线引入到“零输入零状态响应”的输入端。

（2）用示波器的两个探头，一个接输入脉冲信号作同步，一个用于观察输出信号的波形，当脉冲进入低电平阶段时，相当于此时激励去掉，即在低电平时所观察到的波形即为零输入信号。

（3）改变本实验的开关SK900的位置，观察到的是不同情况下的零输入响应，进行相应的比较

3、系统的零状态响应特性观察

（1）观察的方法与上述相同，不过当脉冲进入高电平阶段时，相当于此时加上激励，即此时零状态响应应在脉冲的高电平进行。

（2）改变本实验的开关SK900的位置，观察到的是不同系统下的零输入响应，进行相应的比较。

六、实验报告

1、用两个坐标轴，分别绘制出零输入和零状态的输出波形。

2、通过绘制出的波形，和理论计算的结果进行比较。

七、实验思考题

图2-1-1所示电路中，根据实验提供的实验元件，计算系统的零状态和零输入过程。

八、实验测试点的说明

1、测试点分别为：

“输入”（孔和测试钩）：阶跃信号的输入端。

“输出”：零输入和领状态的输出端。

“GND”：与实验箱的地相连。

2、调节点分别为：

“S9”：此模块的电源开关。

实验二 无失真传输系统

一、实验目的

1、了解无失真传输的概念。

2、了解无失真传输的条件。

二、实验内容

1、观察信号在失真系统中的波形。

2、观察信号在无失真系统中的波形。

三、实验仪器

1、信号与系统实验箱一台（主板）；

2、系统复域与频域的分析模块一块。

3、20M双踪示波器一台。

四、实验原理

1、一般情况下，系统的响应波形和激励波形不相同，信号在传输过程中将产生失真。

线性系统引起的信号失真有两方面因素造成，一是系统对信号中各频率分量幅度产生不同程度的衰减，使响应各频率分量的相对幅度产生变化，引起幅度失真。另一是系统对各频率分量产生的相移不与频率成正比，使响应的各频率分量在时间轴上的相对位置产生变化，引起相位失真。

线性系统的幅度失真与相位失真都不产生新的频率分量。而对于非线性系统则由于其非线性特性对于所传输信号产生非线性失真，非线性失真可能产生新的频率分量。

（4－4）就是对于系统的频率响应特性提出的无失真传输条件。欲使信号在通过线性系统时不产生任何失真，必须在信号的全部频带内，要求系统频率响应的幅度特性是一常数，相位特性是一通过原点的直线。

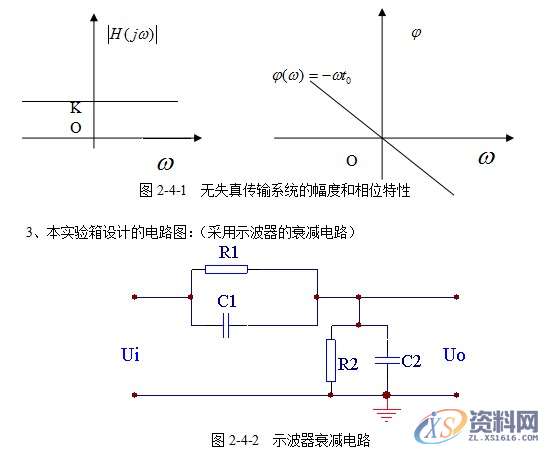
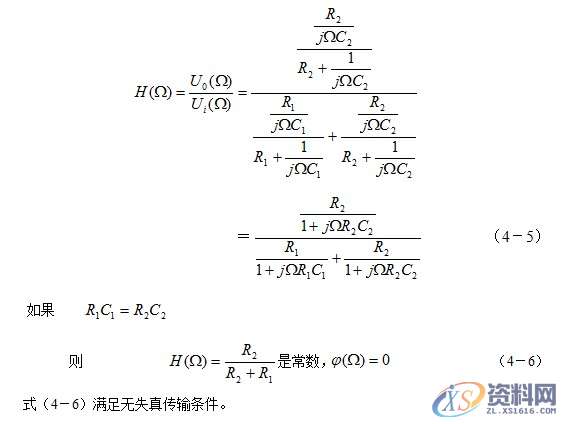
五、实验步骤

1、把系统复域与频域分析模块插在主板上，用导线接通此模块“电源接入”和主板上的电源（看清标识，防止接错，带保护电路），并打开此模块的电源开关。

2、打开函数信号发生器的电源开关，使其输出一方波信号，频率为，峰峰值为，将其接入到此实验模块的输入端，用示波器的两个探头观察，一个接入到输入端，一个接入到输出端，以输入信号作输出同步进行观察。

3、观察信号是否失真，即信号的形状是否发生了变化，如果发生了变化，可以调节电位器“失真调节”，可调节到输出与输入信号的形状一致，只是信号的幅度发生了变化（一般变为原来的两倍）。

4、改变信号源，采用的信号源可以从函数信号发生器引入，也可以从常用信号分类与观察引入各种信号，重复上述的操作，观察信号的失真和非失真的情况。

六、实验报告

1、绘制各种输入信号失真条件下的输入输出信号（至少三种）。

2、绘制各种输入信号无失真条件下的输入输出信号（至少三种）。

七、实验思考题

比较无失真系统与理想低通滤波器的幅频特性和相频特性。

八、实验测试点的说明

1、测试点分别为：

“输入”：模拟信号的输入。

“输出”：模拟信号经过系统后的输出。

“GND”：与实验箱的地相连。

2、调节点分别为：

“失真调节”：调节此电位器，可以观察信号失真的过程。

实验三 二阶系统的特性测量

一、实验目的

1、掌握二阶网络的构成方法。

2、掌握二阶网络的系统响应特性。

3、了解二阶网络波特图的测量方法。

二、实验内容

1、通过阶跃信号观察其阶跃响应。

2、通过正弦信号观察系统的幅频特性，学会绘制波特图。

三、预备知识

了解波特图的绘制。

四、实验仪器

1、信号与系统实验箱一台。

2、二阶系统分析模块一块。

3、20MHz示波器一台。

五、实验原理

1、波特图

频率特性曲线是实际中用的最多的频率特性形式，而波特图则是描述频率特性曲线的一种很好方式，同时波特图提出用对数坐标绘制波特图的 方法，简化了计算和作图。

下面分析波特图的绘制原理：

2、二阶系统

在电路系统中，二阶系统是一阶系统的扩展，与一阶系统一样是构成复杂系统基本单元。一般二阶系统的构成电路如下图：

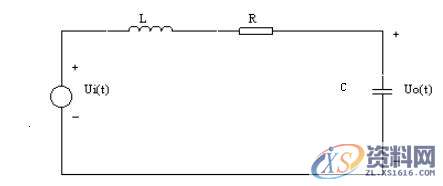
图2-7-1 二阶系统

二阶系统的传输函数一般可以写成：

在二阶系统中ξ为二阶系统的阻尼系数，当0＜ξ＜1时系统处于欠阻尼振荡，其单位冲激响应是一个振荡的过程。当ξ＞1时系统处于过阻尼振荡，其单位冲激响应是一个衰减过程。当ξ＝1时系统处于临界阻尼状态。

二阶网络在不同阻尼状态下的单位冲激响应与单位阶跃响应曲线如下图所示：

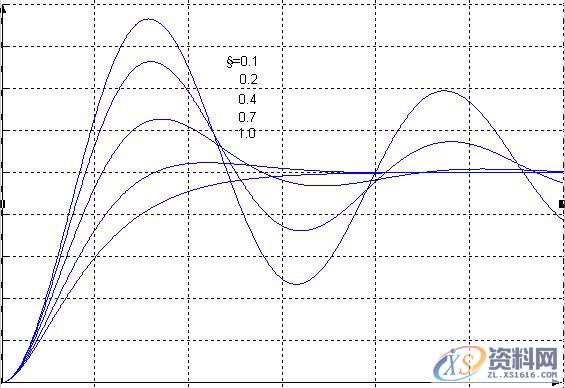
图2-7-2 二阶系统的阶跃响应

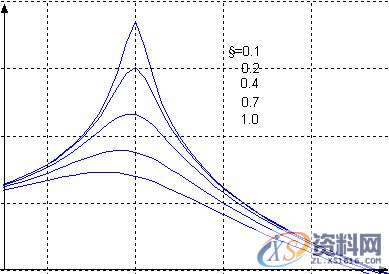
图2-7-3 二阶系统的波特图

实验电路如下图所示：

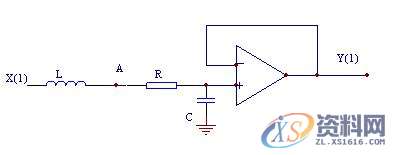
图2-7-4 二阶网络实验电路

六、实验步骤

1、把二阶系统分析模块插在主板上，用导线接通此模块“电源接入”和主板上的电源（看清标识，防止接错，带保护电路），并打开此模块的电源开关。

2、二阶网络单位阶跃响应测量：函数信号发生器模块产生一频率为1KHz，峰峰值为5V左右的方波信号，将方波信号加入到此实验模块的“输入”端。用示波器测量二阶网络的单位阶跃响应，改变系统的阻尼系数，可以观察不同阻尼情况下的阶跃响应。与图2-7-2进行比较。

3、二阶网络波特图的测量

幅频特性的测量：

（1）首先用函数信号发生器模块的频率选择在中频段，“频率调节”选择最小频率（约为1KHz），使其产生一峰峰值为5V左右的正弦信号，加入到此实验模块的插孔“输入”端。

（2）用示波器测量“输出”，观察二阶网络的输出信号。

（3）然后不断增加信号源的输出频率（以二倍频为一步进，即2K、4K、6K……），并保持其输出幅度不变，测量相应频点，并记录下输出信号的幅度、输出信号与输入信号的相位差。以频率与输出幅度（可换算成相对0点的相对电平值，单位为dB）为变量画出一曲线，即为二阶网络的幅频特性。

相频特性的测量：

（1）首先用函数信号发生器模块的频率选择在中频段，“频率调节”选择最小频率（约为1 K），使其产生一峰峰值为5V左右的正弦信号，加入到此实验模块的插孔“输入”端。

（2）用示波器的两个探头测量，一个测输出，一个测输入，用李沙育图的方法观察（以45、90、135、180为特征角度）。

不同系统阻尼情况下的幅频和相频特性：

先使二阶系统工作在欠阻尼状态下，即，进行观察，可以改变系统的工作阻尼状态，测量过阻尼状态的幅频特性和相频特性。

七、实验报告

1、绘制不同阻尼情况下，系统的波特图曲线。

2、绘制不同阻尼情况下，系统的阶跃响应曲线。

八、实验测试点的说明

1、测试点分别为：

“输入”：模拟信号的输入。

“输出”：测试信号的输出。

“GND”：与实验箱上的地相连。

2、调节点分别为：

“S7”：此试验模块的电源开关。

“阻尼系数调节”：，不同的阻尼系数，系统的幅频特性将不同。

实验四 系统稳定性分析

一、实验目的

1、熟悉系统稳定的概念和条件。

2、熟悉判别系统稳定性的Routh判据。

3、了解系统函数零、极点分布对系统时域影响。

二、实验内容

1、当系统的极点在S平面的左平面时，观察系统稳定时的波形。

2、当系统的极点在S平面的右平面时，观察系统非稳定时的波形。

三、预备知识

认识零极图的绘制方法。

四、实验仪器

1、信号与系统实验箱一台（主板）。

2、线性系统综合设计性模块一块。

3、20M双踪示波器一台。

五、实验原理

1、稳定性系统的一种定义如下：若系统对任意的有界输入其零状态响应也是有界的，则称此系统为稳定系统。也可称为有界输入有界输出（BIBO）稳定系统。其可以用以下数学表达式说明

2、稳定性是系统自身的性质之一，系统是否稳定与激励信号的情况无关。系统的冲激响应ht或系统函数HS集中表现了系统的本性，当然，他们也反应了系统是否稳定。判定系统是否稳定，可从时域或S域两方面进行。对于因果系统观察在时间趋于无限大时，T是增长、还是趋于有限值或者消失，这样可以确定系统的稳定性。研究HS在平面中极点分布的位置，也可以很方便的给出有关稳定性的结论。从稳定性考虑，因果系统可划分为稳定系统、不稳定系统、临界稳定（边界稳定）系统三种情况：

（1）稳定系统：如果全部极点落于S左半平面（不包含虚轴），则可以满足

（必要条件）

系统是稳定的。

（2）不稳定系统：如果的极点落于S右半平面，或在虚轴上具有二阶以上的极点，则在足够长的时间以后，仍继续增长，系统是不稳定的。

（3）临界稳定系统：如果的极点落于S平面虚轴上，且只有一阶，则在足够长的时间以后，趋于一个非零的数值或形成一个等幅振荡。这处于上述两种类型的临界情况。

3、Routh判据:

Routh准则：当Routh表中的第一列的全部元素具有相同的符号时，方程的根全部位于S平面的左半部，而其符号改变次数恰好就是具有正实部或位于S平面的右半部的根的个数。

4、参考原理图

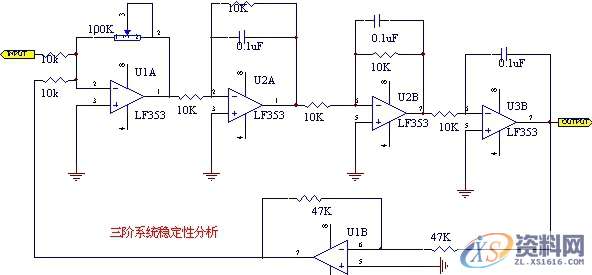
图4-1-1 三阶系统稳定性分析

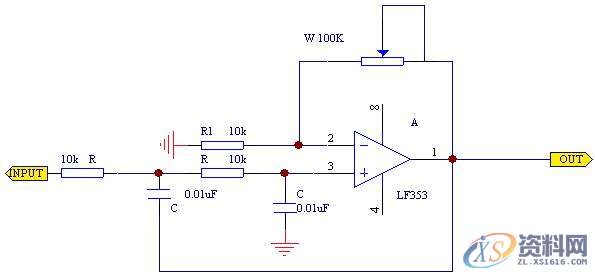
图4-1-2 二阶系统稳定性分析

六、实验步骤

1、二阶系统的稳定性分析。

（1）把线性系统综合分析模块插在主板上，用导线接通此模块“电源接入”和主板上的电源（看清标识，防止接错，带保护电路），并打开此模块的电源开关。

（2）按照原理图搭建电路。打开函数信号发生器的开关，并使其输出一正弦信号，频率约为1,p-p值为5V左右，输入到此电路的INPUT，改变其中的电位器，观察输出信号从稳定到非稳定的过程，具体的表现为有一定幅度的正弦波，变为一幅度为电源幅度的非稳定波形。

2、三阶系统的稳定性分析。

(1) 按照原理图搭建电路，打开函数信号发生器模块的电源开关，使其输出一方波信号，频率为左右，p－p值为10左右，调节其中的电位器，可以观察到信号从一个有一定幅度的信号，变成一个幅值为电源电压的非稳定性信号。

七、实验报告

1、绘制出二、三阶系统的零极图。

2、列写出系统稳定时，其中二、三阶元件必须满足的范围，比较与实际的实验结果有何差异。