数控机床操作教程-(4)轮廓控制原理实验（图文教程）

       插补模块是整个数控系统中一个极其重要的功能模块之一，插补算法的选择将直接影响到系统的精度、速度和加工能力范围。为此，本章将对各种插补原理进行剖析和实验。
　　插补算法很多，可以归纳为两大类：脉冲增量插补算法和数据采样插补算法。
　　脉冲增量插补算法比较简单，比较容易用硬件实现，所以，硬件数控系统较多采用该法，但随着计算机速度的大大提高，也可用软件模拟硬件来实现这类插补。这类插补算法的输出是脉冲形式，并且每次仅产生一个单位的行程增量（即脉冲当量）。脉冲当量一般为0.01mm，较精密的一般取为0.005mm、0.0025mm或0.001mm。显然，脉冲当量愈小，加工精度愈高。
　　脉冲增量插补算法的种类很多，如：数字脉冲乘法器、逐点比较法（最初称为区域判别法）、数据积分法（又称微分分析器ＤＤＡ），比较积分法（包括：单步追踪法、目标点跟踪法即伸雄函数发生器ＳＦＧ等）、矢量判别法、最小偏差法等。
　　数据采样插补算法，又称为时间分割法，它根据程编进给速度将零件轮廓曲线按插补周期分割为一系列微小直线段，然后，将这些微小直线段对应的位置增量数据进行输出，用以控制伺服系统实现坐标轴的进给。显然，这类插补的输出不是单个脉冲，而是一个数字量。这类插补适用于以交、直流伺服电动机作为执行元件的闭环或半闭环数控系统。
　　为了获得良好的插补精度和插补速度，数控研究人员又研制开发了下列插补方案：
　　（1）采用软硬结合的两级插补方案。先由计算机插补软件将加工零件的轮廓段按10-20ms的插补周期分割成若干直线段（称为粗插补过程），然后利用附加的硬件插补器进一步对粗插补送来的直线段进行插补，并输出脉冲（称为精插补过程）。这样，就大大缓和了实时插补和多任务控制之间的矛盾。ＦＡＮＵＣ公司生产的ＳＹＳＴＥＭ-５数控系统就采用了本方案。
　　（2）采用多ＣＰＵ的分布式处理方案。这类系统中，先将数控系统的全部功能划分为几个子功能模块，并分别分配一个独立的ＣＰＵ来完成该子功能，然后由系统软件来协调各个ＣＰＵ之间的工作。如，美国的麦克唐纳．道格拉斯公司的ＡＣＴＲＩＯＮⅢ型数控系统就采用了本方案，它用４台微处理器分别实现输入／输出、轮廓插补和进给速度控制功能、坐标轴伺服功能、数控加工程序编辑和ＣＲＴ显示。
　　这是数控技术发展的一个方向，它具有较高的性价比。
　　（3）采用单台高性能微机方案。现在的微机性能甚至超过了以前的小型机的性能，德国西门子公司的ＳＹＳＴＥＭ-7系统和８１０系统就采用了本方案。本方案正在蓬勃发展之中。
　　限于篇幅，我们从前面所列插补方法中选择几种加以讨论并实验。

第一节　逐点比较法插补原理实验

一、实验目的

1．掌握逐点比较法直线与圆弧插补的基本原理

2．掌握逐点比较法直线插补与圆弧插补的程序编制方法

3．加深对逐点比较法插补的理解

二、实验原理

逐点比较法的基本原理是，在刀具按要求轨迹运动加工零件轮廓的过程中，不断比较刀具与被加工零件轮廓之间的相对位置，并根据比较结果决定下一步的进给方向，使刀具向减小偏差的方向进给（始终只有一个方向）。

一般地，逐点比较法插补过程有四个处理节拍，如图４－１：

（１）偏差判别。判别刀具当前位置相对于给定轮廓的偏差状况；

（２）坐标进给。根据偏差状况，控制相应坐标轴进给一步，使加工点向被加工轮廓靠拢；

（３）重新计算偏差。刀具进给一步后，坐标点位置发生了变化，应按偏差计算公式计算新位置的偏差值；

（４）终点判别。若已经插补到终点，则返回监控，否则重复以上过程。

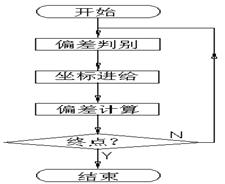
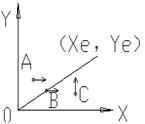
图4-1　处理节拍 　　　 图4-2　第一象限直线插补规律

 １．直线插补

图4-2为第一象限直线，其终点坐标为（Ｘe，Ｙe），现分析其插补规律。

刀尖点位置不外乎３种情况：轮廓线上方（点Ａ），轮廓线上（Ｂ点），轮廓线下方（点Ｃ）。显然，在点Ａ处，为使刀尖点向轮廓直线靠拢，应＋Ｘ向走一步；Ｃ点处，应＋Ｙ向走一步；至于Ｂ点，看来两个方向均可以，但考虑汇编编程时的方便，现规定往＋Ｘ向走一步。

Ａ（Ｘ，Ｙ）点处有：Ｙ／Ｘ>Ｘe／Ｙe ＸeＹ－ＸＹe > 0

Ｂ（Ｘ，Ｙ）点处有：Ｙ／Ｘ＝Ｘe／Ｙe ＸeＹ－ＸＹe ＝ 0

Ｃ（Ｘ，Ｙ）点处有：Ｙ／Ｘ<Ｘe／Ｙe ＸeＹ－ＸＹe < 0

Ｆ＝ＸeＹ－ＸＹe为原始的偏差计算公式（Ｘ，Ｙ为当前插补点动态坐标），Ｆ称为偏差，每走一步到达新位置点，就要计算相应这个Ｆ值。

显然，Ｆ≥0时，须＋Ｘ向走一步；Ｆ＜0时，须＋Ｙ向走一步。为方便汇编编程和提高计算速度，现对偏差Ｆ的计算公式加以简化：

插补点位于Ａ、Ｂ点时，走完下一步（＋Ｘ）：动态坐标变为（Ｘ＝Ｘ＋１，Ｙ＝Ｙ），新偏差变为Ｆ＝ＸeＹ－（Ｘ＋１）Ｙe＝ＸeＹ－ＸＹe－Ｙe＝Ｆ－Ｙe。这个公式比Ｆ＝ＸeＹ－ＸＹe计算要方便。

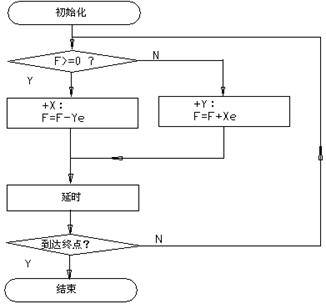
图4-3　逐点比较法第一象限直线插补软件框图

插补点位于Ｃ点时，走完下一步（＋Ｙ）：动态坐标变为（Ｘ＝Ｘ，Ｙ＝Ｙ＋１），新偏差变为Ｆ＝Ｘe（Ｙ＋１）－ＸＹe＝ＸeＹ－ＸＹe＋Ｘe＝Ｆ＋Ｘe。

因此，

走完＋Ｘ后：偏差计算公式为Ｆ＝Ｆ－Ｙe；

走完＋Ｙ后：偏差计算公式为Ｆ＝Ｆ＋Ｘe。

图4-3为逐点比较法第一象限直线插补软件框图。

根据该插补软件框图，可编制逐点比较法第一象限直线插补汇编语言源程序（本程序指令系统采用MCS8031，仅供参考）：

ＬＰ：ＭＯＶ　ＳＰ，＃６０Ｈ　　　定义堆栈指针

　　　ＭＯＶ　４ＡＨ，＃００Ｈ　　偏差单元清零

　　　ＭＯＶ　４９Ｈ，＃００Ｈ

　　　ＭＯＶ　４８Ｈ，＃０１Ｈ　　初始化ＸＹ电动机

　　　ＭＯＶ　４７Ｈ，＃０２Ｈ

　　　ＭＯＶ　Ａ，４ＥＨ　　　　　计算终点判别，Xe+Ye之低位

　　　ＡＤＤ　Ａ，４ＣＨ

　　　ＭＯＶ　５０Ｈ，Ａ

　　　ＭＯＶ　Ａ，４ＤＨ　　　　　Xe+Ye之高位

　　　ＡＤＤＣ　Ａ，４ＢＨ　　　　低位相加，可能产生进位

　　　ＭＯＶ　４ＦＨ，Ａ

　　　ＭＯＶ　Ａ，＃０３Ｈ　　　　ＸＹ电动机上电

　　　ＭＯＶ　ＤＰＴＲ，＃００３０Ｈ

　　　ＭＯＶＸ　＠ＤＰＴＲ，Ａ

ＬＰ２：ＡＣＡＬＬ　ＤＬ０　　　　延时子程序

　　　ＭＯＶ　Ａ，４９Ｈ　　　　　取偏差Ｆ的高８位

　　　ＪＢ　ＡＣＣ．７，ＬＰ４　　偏差Ｆ< 0，去ＬＰ４

　　　ＡＣＡＬＬ　ＸＭＰ　　　　　Ｆ＞＝０，调Ｘ电动机正转子程序

　　　ＣＬＲ　Ｃ　　　　　　　　　计算新偏差Ｆ值，Ｆ＝Ｆ－Ｙe

　　　ＭＯＶ　Ａ，４ＡＨ

　　　ＳＵＢＢ　Ａ，４ＣＨ　　　　可向高位字节借位

　　　ＭＯＶ　４ＡＨ，Ａ

　　　ＭＯＶ　Ａ，４９Ｈ

ＳＵＢＢ　Ａ，４ＢＨ

　　　ＭＯＶ　４９Ｈ，Ａ

ＬＰ３：ＣＬＲ　Ｃ　　　　　　　　终判值减１

　　　ＭＯＶ　Ａ，５０Ｈ

　　　ＳＵＢＢ　Ａ，＃０１Ｈ 可向高位字节借位

　　　ＭＯＶ　５０Ｈ，Ａ

　　　ＭＯＶ　Ａ，４ＦＨ

　　　ＳＵＢＢ　Ａ，＃００Ｈ 考虑低位字节借位

　　　ＭＯＶ　４ＦＨ，Ａ　　　　　终判值判零

　　　ＯＲＬ　Ａ，５０Ｈ　　　　　　

　　　ＪＮＺ　ＬＰ２　　 终判值不为零，去ＬＰ２，否则插补结束

　　　ＬＪＭＰ　００００Ｈ

ＬＰ４：ＡＣＡＬＬ　ＹＭＰ　　　　调Ｙ电动机正转子程序

　　　ＭＯＶ　Ａ，４ＡＨ计算新偏差Ｆ值，Ｆ＝Ｆ＋Ｘe

 　　　ＡＤＤ　Ａ，４ＥＨ

　　　ＭＯＶ　４ＡＨ，Ａ

　　　ＭＯＶ　Ａ，４９Ｈ

　　　ＡＤＤＣ　Ａ，４ＤＨ

　　　ＭＯＶ　４９Ｈ，Ａ

　　　ＳＪＭＰ　ＬＰ３

XMP：MOV A，48H 取X电动机当前状态字

　　　ＣＬＲ　Ｃ 移位法

　　　ＲＲＣ　Ａ

　　　ＲＲＣ　Ａ

　　　ＲＲＣ　Ａ

ＸＭＰ２：ＣＰＬ　Ａ

　　　ＡＮＬ　Ａ，＃４９Ｈ　屏蔽无关位

　　　ＭＯＶ　４８Ｈ，Ａ　　保存Ｘ电动机状态字，作为下次转动的基准

　　　ＯＲＬ　Ａ，４７Ｈ　　保存Ｙ电动机原状态不变

ＸＭＰ４：ＭＯＶ　ＤＰＴＲ，＃００３０Ｈ

　　　ＭＯＶＸ　@ＤＰＴＲ，Ａ

　　　ＲＥＴ

ＸＭＭ：ＭＯＶ　Ａ，４８Ｈ

　　　ＣＬＲ

　　　ＲＬＣ　Ａ

　　　ＲＬＣ　Ａ

　　　ＲＬＣ　Ａ

　　　ＳＪＭＰ　ＸＭＰ２

ＹＭＰ：ＭＯＶ　Ａ，４７Ｈ

　　　ＣＬＲ　Ｃ

　　　ＲＲＣ　Ａ

　　　ＲＲＣ　Ａ

　　　ＲＲＣ　Ａ

ＹＭＰ２：ＣＰＬ　Ａ

　　　ＡＮＬ　Ａ，＃９２Ｈ

　　　ＭＯＶ　４７Ｈ，Ａ

　　　ＯＲＬ　Ａ，４８Ｈ

　　　ＳＪＭＰ　ＸＭＰ４

ＹＭＭ：ＭＯＶ　Ａ，４７Ｈ

　　　ＣＬＲ　Ｃ

　　　ＲＬＣ　Ａ

　　　ＲＬＣ　Ａ

　　　ＲＬＣ　Ａ

　　　ＳＪＭＰ　ＹＭＰ２

说明：１）黑体字模块为软件环形分配器；

　２）各变量地址分配如下：４ＦＨ５０Ｈ－终判值，４ＤＨ４ＥＨ－Ｘe，４ＢＨ４ＣＨ－Ｙe，４９Ｈ４ＡＨ－偏差值Ｆ，４７Ｈ－Ｙ电动机状态字，４８Ｈ－Ｘ电动机状态字；以大地址格式(最低字节地址单元存放最高位数据)存放各种数据；

3）口地址0030H与XY三相步进电动机相线关系如下：

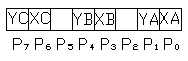
１．１． 圆弧插补

图4-4为第一象限逆圆，现分析其插补规律。

刀尖点位置不外乎３种情况：轮廓线外面（点Ａ），轮廓线上（Ｂ点），轮廓线里面（点Ｃ）。显然，在点Ａ处，为使刀尖点向轮廓圆弧靠拢，应－Ｘ向走一步；Ｃ点处，应＋Ｙ向走一步；至于Ｂ点，看来两个方向均可以，但考虑汇编编程时的方便，现规定往－Ｘ向走一步。

Ａ（Ｘ，Ｙ）点处有：Ｘ2＋Y2＞Ｒ2 　 Ｘ2＋Y2－R2＞0

Ｂ（Ｘ，Ｙ）点处有：Ｘ2＋Y2＝Ｒ2 Ｘ2＋Y2－R2＝0

Ｃ（Ｘ，Ｙ）点处有：Ｘ2＋Y2＜R2 Ｘ2＋Y2－R2＜0

原始的偏差计算公式为：Ｆ＝Ｘ2＋Y2－R2（Ｘ，Ｙ为当前插补点动态坐标）。

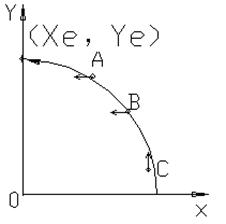
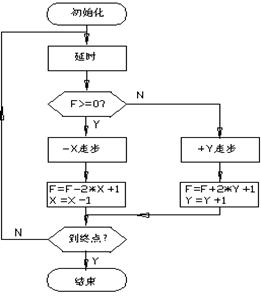
图4-4　第一象限逆圆插补规律 图4-5　逐点比较法第一象限逆圆插补软件框图

显然，Ｆ＜0时，须＋Y向走一步；Ｆ≥0时，须－Ｘ向走一步。为方便汇编编程和提高计算速度，对偏差Ｆ的计算公式加以简化：

插补点位于Ａ、Ｂ点时，走完下一步（－Ｘ）：动态坐标变为（Ｘ＝Ｘ－１，Ｙ＝Ｙ），新偏差变为Ｆ＝（Ｘ－１）²＋Y²－R²＝Ｆ－２Ｘ＋１。

它比公式Ｆ＝Ｘ²＋Y²－R²计算要方便很多。

插补点位于Ｃ点时，走完下一步（＋Ｙ）：动态坐标变为（Ｘ＝Ｘ，Ｙ＝Ｙ＋１），新偏差变为Ｆ＝Ｘ²＋(Y+1)²－R²=Ｆ＋２Ｙ＋１。

因此，

走完－Ｘ后：偏差计算公式为Ｆ＝Ｆ－２Ｘ＋１，动态坐标修正为Ｘ＝Ｘ－１；

走完＋Ｙ后：偏差计算公式为Ｆ＝Ｆ＋２Ｙ＋１，动态坐标修正为Ｙ＝Ｙ＋１。

图４－5为逐点比较法第一象限逆圆插补软件框图。

根据该插补软件框图，编制出逐点比较法第一象限逆圆插补汇编语言源程序（本程序指令系统采用MCS8031，仅供参考）：

ＲＰ：ＭＯＶ　ＳＰ，＃６０Ｈ

　　ＭＯＶ　４ＡＨ，＃００Ｈ Ｆ单元清零

　　ＭＯＶ　４９Ｈ，＃００Ｈ

　　ＭＯＶ　４８Ｈ，＃０１Ｈ　Ｘ电动机初始化

　　ＭＯＶ　４７Ｈ，＃０２Ｈ　Ｙ电动机初始化

 　　ＭＯＶ　ＤＰＴＲ，＃００３０Ｈ

　　ＭＯＶ　Ａ，＃０３Ｈ　　　ＸＹ电动机上电

　　ＭＯＶＸ　@ＤＰＴＲ，Ａ

　　ＣＬＲ　Ｃ　　　　　　　　计算终判值

　　ＭＯＶ　Ａ，５２Ｈ　　　　低位Ｘ、Ｘe相减，得a

　　ＳＵＢＢ　Ａ，４ＥＨ

　　ＭＯＶ　５４Ｈ，Ａ　　　　保存结果于终判值单元低位字节

　　ＭＯＶ　Ａ，５１Ｈ　　　　高位Ｘ、Ｘe相减，得b

　　ＳＵＢＢ　Ａ，４ＤＨ

　　ＭＯＶ　５３Ｈ，Ａ 　　 保存结果于终判值单元高位字节

　　ＣＬＲ　Ｃ 　　低位Ye、Y相减，得c

　　ＭＯＶ　Ａ，４ＣＨ　　

　　ＳＵＢＢ　Ａ，５０Ｈ　

　　ＭＯＶ　２０Ｈ，Ｃ　　　　暂存Ye、Y低位相减产生的借位位

　　ＡＤＤ　Ａ，５４Ｈ　　　　计算d=a+c，d为低位终判值

　　ＭＯＶ　５４Ｈ，Ａ　　　　保存d于终判值单元低位字节

ＭＯＶ　２１Ｈ，Ｃ　　　　暂存d=a+c产生的进位位

ＭＯＶ　Ａ，４ＢＨ　　

ＭＯＶ　Ｃ，２０Ｈ　　　　恢复Ye、Y低位相减产生的借位位

ＳＵＢＢ　Ａ，４ＦＨ　　　高位Ye、Y相减，得e

ＭＯＶ　Ｃ，２１Ｈ 　　恢复d=a+c产生的进位位

ＡＤＤＣ　Ａ，５３Ｈ　　　计算f=b+e，f为高位终判值

ＭＯＶ　５３Ｈ，Ａ　　　　保存f于终判值单元高位字节

　　　　ＲＰ２：ＡＣＡＬＬ　ＤＬ０　　延时子程序

ＭＯＶ　Ａ，４９Ｈ　　　　取Ｆ高位字节　　　　　　　

ＪＢ　ＡＣＣ．７，ＲＰ６　高位＝1，Ｆ＜0，去ＲＰ６

ＡＣＡＬＬ　ＸＭＭ　　　　高位＝０，Ｆ＞0，Ｘ反转一步

ＣＬＲ　Ｃ　　　　　　　　计算新偏差Ｆ＝Ｆ－２Ｘ＋１

ＭＯＶ　Ａ，４ＡＨ　　　　计算g＝Ｆ－Ｘ低位

ＳＵＢＢ　Ａ，５２Ｈ

ＸＣＨ　Ａ，Ｂ　　　　　　g存入Ｂ寄存器

ＭＯＶ　Ａ，４９Ｈ　　　　计算h＝Ｆ－Ｘ高位

ＳＵＢＢ　Ａ，５１Ｈ

ＸＣＨ　Ａ，Ｂ 低位存Ａ，高位存Ｂ。ＢＡ内容为Ｆ－Ｘ

ＣＬＲ　Ｃ　　　　　　　　计算i＝g－Ｘ＝Ｆ－２Ｘ低位

ＳＵＢＢ　Ａ，５２Ｈ　　　　　　

ＸＣＨ　Ａ，Ｂ　　　　　　Ｂ内容为Ｆ－２Ｘ低位，Ａ内容为Ｆ－Ｘ高位

ＳＵＢＢ　Ａ，５１Ｈ　　　Ａ内容为Ｆ－２Ｘ高位

ＸＣＨ　Ａ，Ｂ　　　　　　ＢＡ内容为Ｆ－２Ｘ

ＡＤＤ　Ａ，＃０１Ｈ　　　计算Ｆ－２Ｘ＋１

ＭＯＶ　４ＡＨ，Ａ　　　　４Ａ内容为Ｆ－２Ｘ＋１低位

ＸＣＨ　Ａ，Ｂ　　　　　　Ｂ内容为Ｆ－２Ｘ＋１低位，Ａ内容为Ｆ－２Ｘ高位

ＡＤＤＣ　Ａ，＃００Ｈ　　考虑Ｆ－２Ｘ＋１的进位

ＭＯＶ　４９Ｈ，Ａ　　　　４９Ｈ的内容为Ｆ－２Ｘ＋１高位

ＣＬＲ　Ｃ　　　　　　　　计算Ｘ＝Ｘ－１

ＭＯＶ　Ａ，５２Ｈ 低位

ＳＵＢＢ　Ａ，＃０１Ｈ

ＭＯＶ　５２Ｈ，Ａ

ＭＯＶ　Ａ，５１Ｈ 高位

ＳＵＢＢ　Ａ，＃００Ｈ

ＭＯＶ　５１Ｈ，Ａ

ＲＰ４：ＣＬＲ　Ｃ　　　　　　　终判值减１

　　　ＭＯＶ　Ａ，５４Ｈ

　　　ＳＵＢＢ　Ａ，＃０１Ｈ

　　　ＭＯＶ　５４Ｈ，Ａ

　　　ＭＯＶ　Ａ，５３Ｈ

　　　ＳＵＢＢ　Ａ，＃００Ｈ

　　　ＭＯＶ　５３Ｈ，Ａ

　　　ＯＲＬ　Ａ，５４Ｈ

　　　ＪＮＺ　ＲＰ２　　　　　　插补没结束，转至ＲＰ２

　　　ＬＪＭＰ　００００Ｈ　　

ＲＰ６：ＡＣＡＬＬ　ＹＭＰ　　　Ｙ电动机正转

　　　ＭＯＶ　Ｒ６，＃０２Ｈ 　此处“２”，为“Ｆ＋２Ｙ＋１”的“２”

ＲＰ７：ＭＯＶ　Ａ，４ＡＨ　　　　　　Ｆ＋２Ｙ＋１

　　　ＡＤＤ　Ａ，５０Ｈ

　　　ＭＯＶ　４ＡＨ，Ａ

　　　ＭＯＶ　Ａ，４９Ｈ　　　　　　　

　　　ＡＤＤＣ　Ａ，４ＦＨ
ＭＯＶ　４９Ｈ，Ａ

 　　　ＤＪＮＺ　Ｒ６，ＲＰ７　　　　　

　　　ＭＯＶ　Ａ，４ＡＨ　　　　　　　

　　　ＡＤＤ　Ａ，＃０１Ｈ　　　　　　

　　　ＭＯＶ　４ＡＨ，Ａ

　　　ＭＯＶ　Ａ，４９Ｈ

　　　ＡＤＤＣ　Ａ，＃００Ｈ

　　　ＭＯＶ　Ａ，５０Ｈ

　　　ＡＤＤ　Ａ，＃０１Ｈ

　　　ＭＯＶ　５０Ｈ，Ａ

　　　ＭＯＶ　Ａ，４ＦＨ

　　　ＡＤＤＣ　Ａ，＃００Ｈ

　　　ＭＯＶ　４ＦＨ，Ａ

　　　ＡＪＭＰ　ＲＰ４

说明：１）数据存放格式同前；

　　２）各变量地址分配如下：４７Ｈ－４ＥＨ，存放数据方式同直线，４ＦＨ５０Ｈ－Ｙ，５１Ｈ５２Ｈ－Ｘ，５３Ｈ５４Ｈ－终判值

从逐点比较法的插补原理可知：本法不易实现三轴以上的联动。因此，一般用于数控车床等两轴联动的系统。

为了让没有条件的教学单位也能做实验，此处用VB和C语言改写上述程序，改写后可在计算机屏幕上模拟仿真插补过程。

２．２． 参考程序

VB程序：

直线：

Sub 偏差计算()

偏差 = Abs(x终点) × z动点 - x动点 × Abs(z终点)

End Sub

Sub 插补()

Dim c As Integer

Select Case 象限标志

Case 1: ''第一象限插补

Do Until x动点 + z动点 >= 总步数

If 偏差 >= 0 Then

x动点 = x动点 + 1:

Line -Step(0, x步长), vbRed

Else

z动点 = z动点 + 1:

Line -Step(z步长, 0), vbRed

End If

偏差计算

Loop

Case 2: ''第二象限插补

c = x终点: x终点= z终点: z终点= -c

c = x步长: x步长 = z步长: z步长 = -c

Do Until x动点 + z动点 >= 总步数

If 偏差 >= 0 Then

x动点 = x动点 + 1:

Line -Step(x步长, 0), vbRed

Else

z动点 = z动点 + 1:

Line -Step(0, z步长), vbRed

End If

偏差计算

Loop

Case 3: ''第三象限插补

x步长 = -x步长: z步长 = -z步长

Do Until x动点 + z动点 >= 总步数

If 偏差 >= 0 Then

x动点 = x动点 + 1:

Line -Step(0, x步长), vbRed

Else

z动点 = z动点 + 1:

Line -Step(z步长, 0), vbRed

End If

偏差计算

Loop

Case 4: ''第四象限插补

c = x终点: x终点= -z终点: z终点 = c

c = x步长: x步长 = -z步长: z步长 = c

Do Until x动点 + z动点 >= 总步数

If 偏差 >= 0 Then

x动点 = x动点 + 1: Line -Step(x步长, 0), vbRed

Else

z动点 = z动点 + 1: Line -Step(0, z步长), vbRed

End If

偏差计算

Loop

End Select

End Sub

圆弧：

Sub 偏差计算()

偏差 = Sqr((x动点 - x圆心) 2 + (z动点 - z圆心) 2) - R

End Sub

Sub 插补()

x动点 = x起点: z动点 = z起点:

动点象限判别

xx: Select Case 象限标志

Case 1: 单步连续判断

If 顺逆标志 = "顺" Then ''第一象限插补

Do Until (x动点 - x终点) = 0 And (z动点 - z终点) = 0

If 偏差 >= 0 Then

x动点 = x动点 - 1:

Line -Step(0, -x步长), vbRed

Else

z动点 = z动点 + 1:

Line -Step(z步长, 0), vbRed

End If

偏差计算

动点象限判别

If 象限标志 <> 1 Then

GoTo xx

End If

单步连续判断

Loop

ElseIf 顺逆标志 = "逆" Then

Do Until (x动点 - x终点) = 0 And (z动点 - z终点) = 0

If 偏差 >= 0 Then

z动点 = z动点 - 1:

Line -Step(-z步长, 0), vbRed

Else

x动点 = x动点 + 1:

Line -Step(0, x步长), vbRed

End If

DoEvents

偏差计算

动点象限判别

If 象限标志 <> 1 Then

GoTo xx

End If

Loop

End If

Case 2:单步连续判断

 If 顺逆标志 = "顺" Then ''第二象限插补

Do Until (x动点 - x终点) = 0 And (z动点 - z终点) = 0

If 偏差 >= 0 Then

z动点 = z动点 - 1:

Line -Step(-z步长, 0), vbRed

Else

x动点 = x动点 - 1:

Line -Step(0, -x步长), vbRed

End If

偏差计算

动点象限判别

If 象限标志 <> 2 Then

GoTo xx

End If

Loop

ElseIf 顺逆标志 = "逆" Then

Do Until (x动点 - x终点) = 0 And (z动点 - z终点) = 0

If 偏差 >= 0 Then

x动点 = x动点 + 1:

Line -Step(0, x步长), vbRed

Else

z动点 = z动点 + 1:

Line -Step(z步长, 0), vbRed

End If

偏差计算

动点象限判别

If 象限标志 <> 2 Then

GoTo xx

End If

Loop

End If

Case 3: 单步连续判断

If 顺逆标志 = "顺" Then ''第三象限插补

Do Until (x动点 - x终点) = 0 And (z动点 - z终点) = 0

If 偏差 >= 0 Then

x动点 = x动点 + 1:

Line -Step(0, x步长), vbRed

Else

z动点 = z动点 - 1:

Line -Step(-z步长, 0), vbRed

End If

DoEvents

偏差计算

动点象限判别

If 象限标志 <> 3 Then

GoTo xx

End If

Loop

ElseIf 顺逆标志 = "逆" Then

Do Until (x动点 - x终点) = 0 And (z动点 - z终点) = 0

If 偏差 >= 0 Then

z动点 = z动点 + 1:

Line -Step(z步长, 0), vbRed

Else

x动点 = x动点 - 1:

Line -Step(0, -x步长), vbRed

End If

偏差计算

动点象限判别

If 象限标志 <> 3 Then

GoTo xx

End If

Loop

End If

Case 4: 单步连续判断

If 顺逆标志 = "顺" Then ''第三象限插补

Do Until (x动点 - x终点) = 0 And (z动点 - z终点) = 0

If 偏差 >= 0 Then

z动点 = z动点 + 1:

Line -Step(z步长, 0), vbRed

Else

x动点 = x动点 + 1:

Line -Step(0, x步长), vbRed

End If

偏差计算

动点象限判别

If 象限标志 <> 4 Then

GoTo xx

End If

Loop

ElseIf 顺逆标志 = "逆" Then

Do Until (x动点 - x终点) = 0 And (z动点 - z终点) = 0

If 偏差 >= 0 Then

x动点 = x动点 - 1:

Line -Step(0, -x步长), vbRed

Else

z动点 = z动点 - 1:

Line -Step(-z步长, 0), vbRed

End If

偏差计算

动点象限判别

If 象限标志 <> 4 Then

GoTo xx

End If

Loop

End If

End Select

End Sub

C程序：

#include "conio.h"

#include "graphics.h"

#include "process.h"

#define Ni_circle 0

#define Shun_circle 1

void init_graph();

void draw_Base_circle();

void draw_cabu_circle();

void close_graph();

void acrroods();

static float x0,y0;

void line_cabu(), draw_line(),draw_line_cabu();

void line_cabu() /*此函数控制直线插步两次*/

{

int i;

init_graph();

sleep(1);

for(i=0;i<2;i++)

{

line(0,120,300,120); outtextxy(310,120,"Z");

line(100,10,100,300); outtextxy(110,300,"X");

outtextxy(90,130,"O");

draw_line();

if(i==0)

draw_line_cabu(6);

else draw_line_cabu(2);

gotoxy(50,5);

getch();

cleardevice();

setcolor(WHITE);

}

}

void draw_line()/*画直线*/

{

line(100,120,600,450);

textcolor(YELLOW);

directvideo=0;

gotoxy(45,5); cprintf("Line from:X0 Y0 Z0 ");

gotoxy(45,6); cprintf("Line to :X500 Y0 Z330");

gotoxy(45,7); cprintf("Units :Pixel");

gotoxy(45,8); cprintf("Line now:");

}

void draw_line_cabu(int step)/*关键的直线插补函数*/

{

int Xe=600,Ye=450;

float Fm,Xm=100,Ym=120;

setcolor(RED);

moveto(Xm,Ym);

while(Xm<=Xe&&Ym<=Ye)

{

Fm=(Ym-120)*(Xe-100)-(Xm-100)*(Ye-120);

if(Fm>=0)

Xm=Xm+step;

else

Ym=Ym+step;

lineto(Xm,Ym);

gotoxy(55,8); printf("X%3.0f Y0 Z%3.0f",Xm-100,Ym-120);

delay(1100);

}

}

/* 圆插补部分的函数区*/

void init_graph() /*图形系统初始化*/

{

int gdrive=DETECT,gmode;

initgraph(&gdrive,&gmode,"");

cleardevice();

}

void acrroods() /*屏幕中心坐标*/

{

x0=getmaxx()/2;

y0=getmaxy()/2;

}

void draw_Base_circle() /*画圆及写参数*/

{

line(x0-200,y0,x0+200,y0); outtextxy(x0+220,y0,"Z");

line(x0,y0-180,x0,y0+180); outtextxy(x0+10,y0+180,"X");

outtextxy(x0-10,y0+10,"O");

circle(x0,y0,150);

textcolor(YELLOW);

directvideo=0;

gotoxy(46,2);cprintf("Circle start:X0 Y0 Z150");

gotoxy(46,3);cprintf("Circle end :X0 Y0 Z150");

gotoxy(46,4);cprintf("Units :Pixel");

gotoxy(46,5);cprintf("Circle now:");

}

void close_graph() /*关图形系统*/

{

closegraph();

}

void draw_cabu_circle(int sstep,int Directory)/*关键的圆插补函数*/

{

int flag=0;

float Fm,Xm,Ym;

Xm=x0+150; Ym=y0;

moveto(Xm,Ym);

setcolor(RED);

while(1) /*分象限，顺圆和逆圆讨论*/

{

Fm=(Xm-x0)*(Xm-x0)+(Ym-y0)*(Ym-y0)-150*150;/*圆判断公式*/

if(Fm>=0){

if(!Directory){ /*逆圆判断*/

if(Xm>=x0&&Ym<=y0)

{

if(flag) break; /*if语句判断象限，以下一样*/

else Xm=Xm-sstep;

}

if(Xm<=x0&&Ym<=y0)

{

flag=1; Ym=Ym+sstep;

}

if(Xm<=x0&&Ym>=y0)

Xm=Xm+sstep;

if(Xm>=x0&&Ym>=y0)

Ym=Ym-sstep;

}

else { /*it is Directory''s else*/

if(Xm>x0&&Ym

Ym=Ym+sstep;

if(Xm<=x0&&Ym<=y0)

Xm=Xm+sstep;

if(Xmy0) {&&ym>

&&ym>flag=1; Ym=Ym-sstep;}

if(Xm>=x0&&Ym>=y0) {

if(flag) break;

Xm=Xm-sstep;}

}

}

else{ /*it is Fm''s else*/

if(!Directory) {

if(Xm>x0&&Ym

{

if(flag) break;

else Ym=Ym-sstep;

}

if(Xm<=x0&&Ym<=y0)

{

flag=1; Xm=Xm-sstep;

}

if(Xm<=x0&&Ym>=y0)

Ym=Ym+sstep;

if(Xm>=x0&&Ym>=y0)

Xm=Xm+sstep;

}

else{

if(Xm>x0&&Ym

Xm=Xm+sstep;

if(Xm<=x0&&Ym<=y0)

Ym=Ym-sstep;

if(Xm<=x0&&Ym>=y0){

flag=1; Xm=Xm-sstep;}

if(Xm>=x0&&Ym>=y0) {

if(flag) break;

else Ym=Ym+sstep;}

}

}

lineto(Xm,Ym);

gotoxy(58,5); printf("X%3.0f Y0 Z%3.0f ",Ym-y0,Xm-x0);

delay(800);

}

}

void circle_demo(int Directory) /*控制圆插补两次*/

{

int i=0,sstep;

init_graph();

sleep(2);

acrroods(&x0,&y0);

for(i=0;i<2;i++)

{

draw_Base_circle(150);

if(i==0){

sstep=6;

draw_cabu_circle(sstep,Directory);}

else{

sstep=1;

draw_cabu_circle(sstep,Directory);}

getch();

cleardevice();

setcolor(WHITE);

}

}

/* 圆插补部分的函数区结束*/

main()/*主函数负责写封面和函数调用*/

{

int choice=0;

init_graph();

while(choice!=4)

{

setfillstyle(1,RED);

bar(200,30,400,80);

setcolor(GREEN);

settextstyle(3,0,10);

outtextxy(220,50,"DEMO PROGRAM BY P.Y.F");

setcolor(WHITE);

settextstyle(0,0,1);

outtextxy(200,120,"1. Line demo.");

outtextxy(200,140,"2. Shun_Circle demo.");

outtextxy(200,160,"3. Ni_Circle demo.");

outtextxy(200,180,"4. Quit the program.");

outtextxy(160,200,"Please enter your choice:"); gotoxy(46,13);

scanf("%d",&choice);

switch(choice)

{

case 1: line_cabu();break;

case 2: circle_demo(Ni_circle);break;

case 3: circle_demo(Shun_circle);break;

case 4: break;

default: printf("\nChoice wrong,try again!");

}

}

close_graph();

}

三、实验步骤

为了方便教学工作，作者承担了“数控技术远程教育网”网站的部分建设工作，ＵＲＬ为http://dali.3322.net/。可以在雅虎、搜狐和中国教育科研网中找到该站，常年联系电子信箱:zqrong@pub.cz.jsinfo.net。

１．下载文件：CNC-V2.0，这是一个自解压文件（网站可能经常变动），建议你的计算机在运行前安装ＶＢ６．０或其运行库。

２．启动CNC-V2.0后，进入插补界面（图４－６）：

３．根据界面，选择直线插补或圆弧插补。现以圆弧插补为例：

在主界面上选择圆弧插补后，进入圆弧插补界面。单击开始，就可清楚显示圆弧插补轨迹，修改左边的数据，可得到不同圆弧的插补轨迹。还可单步执行，让学员可以对照右上方坐标进行分析。如果圆弧半径相对于脉冲当量很大，那么，根本就看不到插补折线了，对于直线插补，操作与圆弧插补基本相似，参见（图４－７、４－８、４－９、４－１０）。

图4-6　逐点比较法插补主页面

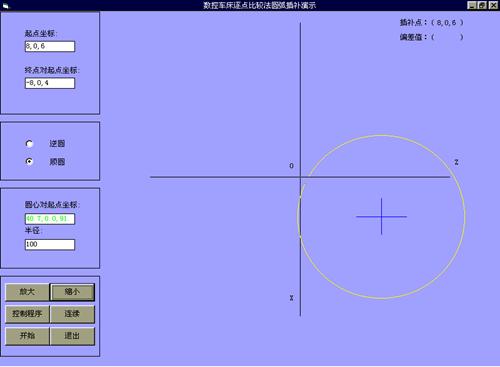
图4-7　逐点比较法圆弧插补界面

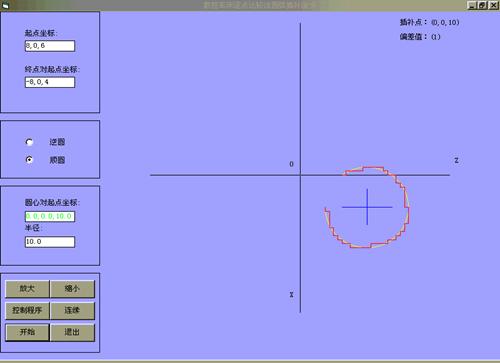
图4-8　逐点比较法圆弧插补演示（一）

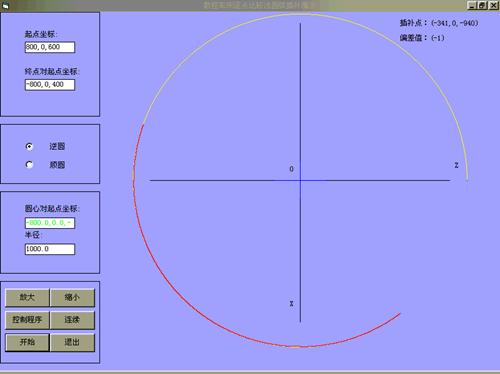
图4-9　逐点比较法圆弧插补演示（二）

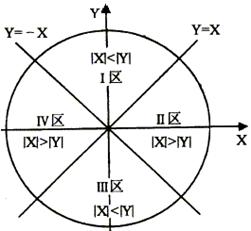
图4-10　逐点比较法直线插补演示

第二节 数字积分法插补原理实验

一、实验目的

１．掌握数字积分法直线与圆弧插补的基本原理

２．掌握数字积分法直线插补与圆弧插补的程序编制方法

３．加深对数字积分法插补的理解

二、实验原理

数字积分法的基本原理是，使用一系列的小矩形面积之和来近似轮廓曲线函数积分的整个面积。此处为方便理解，从物理上来进行ＤＤＡ插补的分析。

1．直线插补

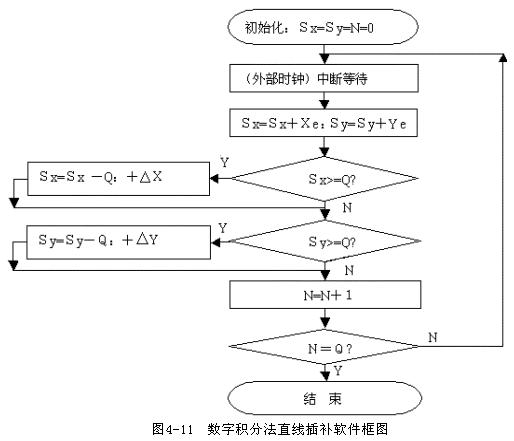
设直线的终点坐标为（Xe，Ye），现取容器两个：Qx和Qy，其容量相等，均为Q≥MAX（Xe，Ye）。按一定的节拍不断将Xe值加入Qx，同时将Ye值加入Qy；若Qx中的值超过Q，则在X方向发一个脉冲，若Qy中的值超过Q，则在Y方向发一个脉冲，注意，两个方向发脉冲的过程是相互独立的事件。显然，若Xe＞Ye，则X方向脉冲发得较快；若Xe＝Ye，则两个方向脉冲发得一样快；若Ye＞Xe，则Y方向脉冲发得较快。

可得软件框图如下(图4-11)。

实际上，数字积分直线插补的物理意义是使插补点沿着速度矢量的方向上进给，对于圆弧插补，这同样适用。

2．圆弧插补

圆弧ＤＤＡ插补与直线ＤＤＡ插补有以下不同：

（1）直线插补时为常量（终点坐标）累加，圆弧插补时为变量（动点坐标）累加。

（2）直线插补时，Qx中放的是终点X坐标，Qy中放的是终点Y坐标；而圆弧插补时，Qx中放的是动点Y坐标，Qy中放的是动点X坐标。

可得圆弧ＤＤＡ插补的软件框图(图４-１２)。

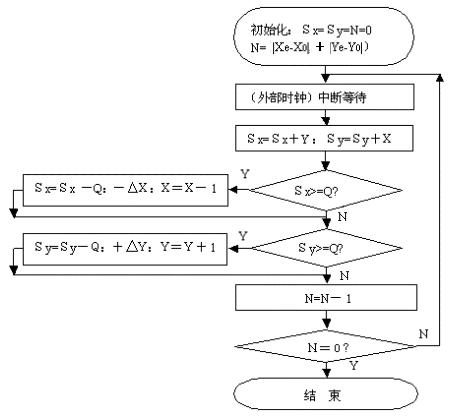
图4-12　数字积分法圆弧插补软件框图

3．参考程序

直线：

Sub 插补X()

标志X = 0

If 余数X >= Q Then

余数X = 余数X Mod Q

x动点 = x动点 + 1: 标志X = 1

End If

End Sub

Sub 插补Y()

标志Y = 0

If 余数Y >= Q Then

余数Y = 余数Y Mod Q

y动点 = y动点 + 1: 标志Y = 1

End If

End Sub

Sub 插补Z()

标志Z = 0

If 余数Z >= Q Then

余数Z = 余数Z Mod Q

z动点 = z动点 + 1: 标志Z = 1

End If

End Sub

Sub 插补公共()

余数X = 余数X + x终点

余数Y = 余数Y + y终点

余数Z = 余数Z + z终点

插补X

插补Y

插补Z

插补记录 = 插补记录 + 1

End Sub

Sub 插补()

Dim c As Integer

插补记录 = 0: 余数X = 0: 余数Y = 0: 余数Z = 0: 划轮廓线

PSet (z原点, x原点), vbRed

Select Case 象限标志

Case 1: ''第一象限插补

Do Until 插补记录 = Q

插补公共

Line -Step(z步长 × 标志Z, x步长 × 标志X), vbRed

Loop

Case 2: ''第二象限插补

c = x终点: x终点 = z终点: z终点 = -c

c = x步长: x步长 = z步长: z步长 = -c

Do Until 插补记录 = Q

插补公共

Line -Step(x步长 × 标志X, z步长 × 标志Z), vbRed

Loop

Case 3: ''第三象限插补

x终点 = -x终点: z终点 = -z终点

x步长 = -x步长: z步长 = -z步长

Do Until 插补记录 = Q

插补公共

Line -Step(z步长 × 标志Z, x步长 × 标志X), vbRed

Loop

Case 4: ''第四象限插补

c = x终点: x终点 = -z终点: z终点 = c

c = x步长: x步长 = -z步长: z步长 = c

Do Until 插补记录 = Q

插补公共

Line -Step(x步长 × 标志X, z步长 × 标志Z), vbRed

Loop

End Select

End Sub

圆弧：

Sub 插补()

PSet (z原点, x原点), vbRed

余数X = 0: 余数Y = 0: 余数Z = 0: 插补记录 = 0:

过象限标志 = 0: 跨象限数量 = 0

If Opt逆圆 = False Then

xx: 跨象限数量 = 跨象限数量 + 1

Select Case 象限标志

Case 1: ''第一象限插补

过象限预处理

Do Until (x动点对圆心 - x终点对圆心) ^ 2 + (z动点对圆心 - z终点对圆心) ^ 2 <= 跨象限数量 ^ 2

If x动点对圆心 = 0 Then

象限标志 = 2:

过象限标志 = 1

GoTo xx

End If

插补公共

Line -Step(z步长 × 标志Z, -x步长 × 标志X), vbRed

Loop

过象限标志 = 0

Case 2: ''第二象限插补

过象限预处理

Do Until (x动点对圆心 - x终点对圆心) ^ 2 + (z动点对圆心 - z终点对圆心) ^ 2 <= 跨象限数量 ^ 2

If x动点对圆心 = 0 Then

象限标志 = 3:

过象限标志 = 1

GoTo xx

End If

插补公共

Line -Step(-x步长 × 标志X, z步长 × 标志Z), vbRed

Loop

过象限标志 = 0

Case 3: ''第三象限插补

过象限预处理

Do Until (x动点对圆心 - x终点对圆心) ^ 2 + (z动点对圆心 - z终点对圆心) ^ 2 <= 跨象限数量 ^ 2

If x动点对圆心 = 0 Then

象限标志 = 4:

过象限标志 = 1

GoTo xx

End If

插补公共

Line -Step(z步长 × 标志Z, -x步长 × 标志X), vbRed

Loop

过象限标志 = 0

Case 4: ''第四象限插补

过象限预处理

Do Until (x动点对圆心 - x终点对圆心) ^ 2 + (z动点对圆心 - z终点对圆心) ^ 2 <= 跨象限数量 ^ 2

If x动点对圆心 = 0 Then

象限标志 = 1:

过象限标志 = 1

GoTo xx

End If

插补公共

Line -Step(-x步长 × 标志X, z步长 ×标志Z), vbRed

 Loop

过象限标志 = 0

End Select

Else

xy: 跨象限数量 = 跨象限数量 + 1

Select Case 象限标志

Case 1: ''第一象限插补

过象限预处理

Do Until (x动点对圆心 - x终点对圆心) ^ 2 + (z动点对圆心 - z终点对圆心) ^ 2 <= 跨象限数量 ^ 2

单步连续判断

If z动点对圆心 = 0 Then

象限标志 = 4:

过象限标志 = 1

GoTo xy

End If

插补公共

Line -Step(-z步长 × 标志Z, x步长 × 标志X), vbRed

Loop

过象限标志 = 0

Case 2: ''第二象限插补

过象限预处理

Do Until (x动点对圆心 - x终点对圆心) ^ 2 + (z动点对圆心 - z终点对圆心) ^ 2 <= 跨象限数量 ^ 2

单步连续判断

If z动点对圆心 = 0 Then

象限标志 = 1:

过象限标志 = 1

GoTo xy

End If

插补公共

Line -Step(x步长 × 标志X, -z步长 × 标志Z), vbRed

Loop

过象限标志 = 0

Case 3: ''第三象限插补

过象限预处理

Do Until (x动点对圆心 - x终点对圆心) ^ 2 + (z动点对圆心 - z终点对圆心) ^ 2 <= 跨象限数量 ^ 2

If z动点对圆心 = 0 Then

象限标志 = 2:

过象限标志 = 1

GoTo xy

End If

插补公共

Line -Step(-z步长 × 标志Z, x步长 × 标志X), vbRed

Loop

过象限标志 = 0

Case 4: ''第四象限插补

过象限预处理

Do Until (x动点对圆心 - x终点对圆心) ^ 2 + (z动点对圆心 - z终点对圆心) ^ 2 <= 跨象限数量 ^ 2

If z动点对圆心 = 0 Then

象限标志 = 3:

过象限标志 = 1

GoTo xy

End If

插补公共

Line -Step(x步长 × 标志X, -z步长 × 标志Z), vbRed

Loop

过象限标志 = 0

End Select

cc: End If

End Sub

三、实验步骤

1．启动CNC-V2.0后，进入如图界面（图４-１３）：

2．根据界面，选择直线插补或圆弧插补。现以圆弧插补为例：

在主界面上选择圆弧插补后，进入圆弧插补界面。单击开始，就可清楚显示圆弧插补轨迹，修改左边的数据，可得到不同圆弧的插补轨迹。还可单步执行，让学员可以对照右上方坐标进行分析。如果圆弧半径相对于脉冲当量很大，那么，根本就看不到插补折线了，对于直线插补，操作与圆弧插补基本相似。参见图４－１４、４－１５、４－１６、４－１７。

注意：当标尺值小于圆弧的半径时，数字积分法插补出带圆角的正方形，若标尺值是零，则该正方形的圆角不存在，见图４－１６。

图4-13　数字积分法插补主页面

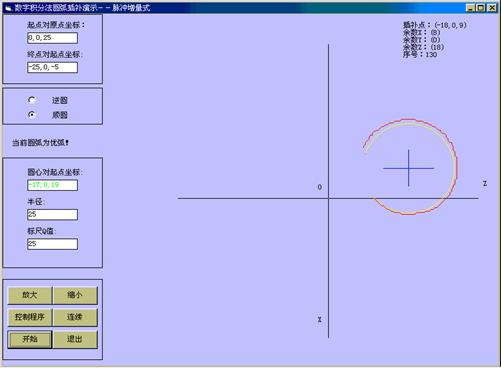
图4-14　数字积分法圆弧插补演示（一）

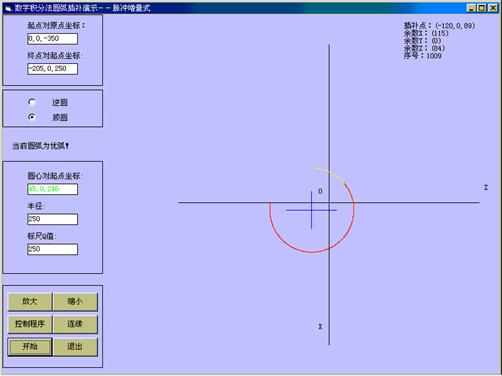
图4-15　数字积分法圆弧插补演示（二）

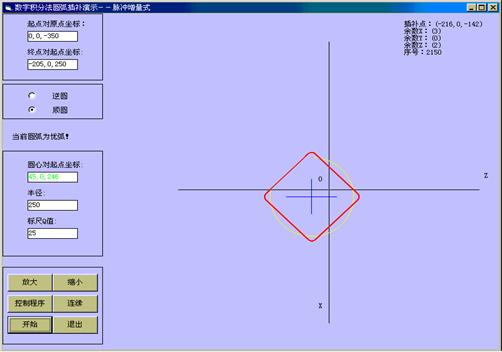
图4-16　数字积分法圆弧插补演示（三）

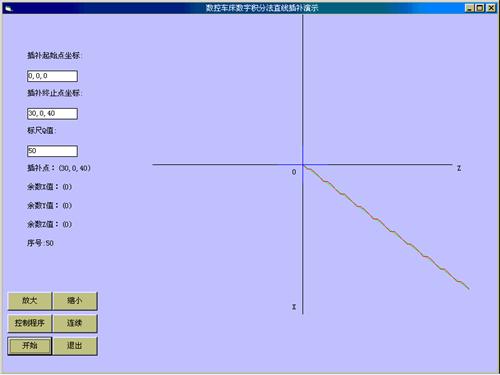
图4-17　数字积分法直线插补演示

第三节 数据采样法插补原理实验

　　一、实验目的

1．掌握数据采样法直线与圆弧插补的基本原理

2．了解数据采样法直线插补与圆弧插补的程序编制方法

3．加深对数据采样法插补的理解

二、实验原理

随着数控系统中计算机的引入，插补实时性和计算复杂性之间的矛盾已不再那么突出了。因此，现代数控系统中就采用了结合计算机采样思想的数据采样插补法。

数据采样法实际上是一种粗插补过程，它所产生的微小线段仍然比较大，必须进一步对其密化（即精插补）。粗插补算法较复杂，大多用高级语言编制；精插补算法较简单，多用汇编语言或硬件插补器实现。

粗插补产生微小线段的周期称为插补周期Ts，精插补的周期称为位置控制周期Ｔc，它是伺服位置环的采样控制周期。对于特定的系统，Ｔs、Ｔc是两个固定不变的时间参数，且Ｔs＝nＴc，n为自然数。

Ｔs对系统稳定性没有影响，但对被加工轮廓的轨迹精度有影响，Ｔs愈大，则产生的微小线段愈长（△Ｌ＝ＦＴs，Ｆ为程编速度），插补计算误差就愈大。而Ｔc对系统稳定性和被加工轮廓的轨迹精度都有影响。

 可见，为减小插补误差，应尽量减小Ｔs，但Ｔs若太小，则ＣＰＵ可能来不及进行位置计算、显示、监控、Ｉ／Ｏ处理等ＣＮＣ任务，Ｔs必须大于插补运行时间和完成其他相关

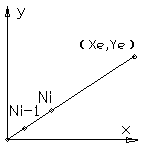
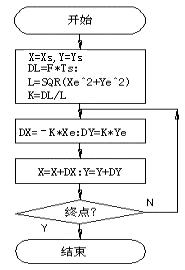
图４-18　第一象限直线　 图４-19　第一象限数据采样直线插补软件流程图

任务所需时间之和。目前，Ｔs一般在１０ms左右，如美国ＡＢ公司的７３６０ＣＮＣ系统，Ｔs＝１０．２４ms；德国ＳＩＥＭＥＮＳ公司的System－7CNC系统，Ｔs＝８ms。随着计算机速度的提高，Ｔs有减小的趋势。

Ｔc选择一般有两种情况：Ｔc＝Ｔs（７３６０ＣＮＣ系统），Ｔc＝０.５Ｔs（System－7CNC系统）。

以上是数据采样法的基本原理，下面讨论插补具体轮廓线时的情形。

１．１． 直线插补

图４－１８为第一象限直线，现分析其插补规律。

刀尖从点Ｎi-1移动到点Ｎi，沿轮廓直线方向的增量为ＤＬ＝Ｆ×Ｔs，沿Ｘ向的增量为ＤＸ，沿Ｙ向的增量为ＤＹ，它们之间的关系是：

ＤＸ＝ＤＬ×Ｘe／Ｌ，ＤＹ＝ＤＬ×Ｙe／Ｌ

其中，Ｌ为轮廓直线的长度，它满足等式：Ｌ²＝Ｘe²+Ｙe²

Ｎi点的动态坐标可以用前一个点的坐标动态表示：Ｘ＝Ｘ＋ＤＸ，Ｙ＝Ｙ＋ＤＹ

由此，可设计第一象限数据采样直线插补软件流程图，见图４－１９。

２．２． 圆弧插补

数据采样法圆弧插补的基本思路是在满足加工精度的前提下，用切线、弦线或割线来代替圆弧实现进给，即用直线逼近圆弧。

（1）切线法（一阶ＤＤＡ算法）

　　图4-20为第一象限逆圆，现分析其切线法插补规律。

　　设当前点在Ni－1，按切线方向前进一个粗插补周期后到达Ｎi点，走过的粗插补

单位长度为 Ｌ＝Ｆ×Ｔs，其中：Ｆ为进给速度，粗插补周期为Ｔs。

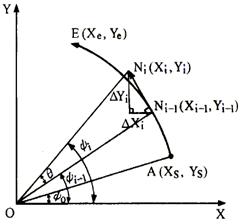
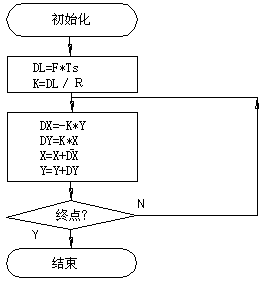
图４-20　切线法逆圆插补示意图 　　　图４-21切线法圆弧插补流程图

显然，Ｘi－1＝Ｒcosψi－1　　　（Ｒ为圆弧半径）

　　　　Ｙi－1＝Ｒsinψi－1

　　　　Ｘi＝Ｒcos（ψi－1＋θ）

Ｙi＝Ｒsin（ψi－1＋θ）

从而

　　　Ｘi＝Ｘi－1cosθ－Ｙi－1 sinθ

　　　Ｙi＝Ｙi－1cosθ＋Ｘi－1 sinθ

因θ很小，所以

sinθ＝θ－θ³/3!＋θ⁵/5!－……

　　　cosθ＝1－θ²/２!＋θ⁴/４!－……

取一阶近似（一阶ＤＤＡ名称的由来），得

　　　sinθ＝θ＝Ｆ×Ｔs／Ｒ＝Ｋ

　　　cosθ＝1

因此

　　　Ｘi＝Ｘi－1－ＫＹi－1

Ｙi＝Ｙi－1＋ＫＸi－1

　　Ｘi＝Ｘi－Ｘi－1＝－ＫＹi－1

　　Ｙi＝Ｙi－Ｙi－1＝ＫＸi－1

　　　由此，可设计第一象限切线法数据采样圆弧插补软件流程图，见图４－２１。

本法与脉冲增量方式ＤＤＡ插补在本质上是相同的，前者是后者的推广。由于误差太大（可以在随后的实验中验证），在实际的CNC系统中并不使用。

（2）弦线法（直接函数算法）

图4-22为第一象限顺圆，弦线法插补规律（请参考有关书籍自行分析）如下：

Ⅰ区：

　　　∆Ｘi＝（Ｙi－1＋∆Ｙi－1×０.５）×ＦＴs／Ｒ

　　　∆Ｙi＝－Ｙi－1＋（Ｒ²－（Ｘi－１＋∆Ｘi）²）^1/2

　　 Ｘi＝Ｘi－１＋∆Ｘi

Ｙi＝Ｙi－１＋∆Ｙi

Ⅱ区：

　　　∆Ｙi＝（Ｘi－1＋∆Ｘi－1×０.５）×ＦＴs／Ｒ

　　　∆Ｘi＝－Ｘi－1＋（Ｒ²－（Ｙi－１＋∆Ｙi）²）^1/2

　　 Ｘi＝Ｘi－１＋∆Ｘi

Ｙi＝Ｙi－１＋∆Ｙi

Ⅲ区：

　　　∆Ｘi＝（Ｙi－1＋∆Ｙi－1×０.５）×ＦＴs／Ｒ#8710;Ｙi＝－Ｙi－1—（Ｒ²－（Ｘi－１＋∆Ｘi）²）^1/2

　　 Ｘi＝Ｘi－１＋∆Ｘi

Ｙi＝Ｙi－１＋∆Ｙi

Ⅳ区：

　　　∆Ｙi＝（Ｘi－1＋∆Ｘi－1×０.５）×ＦＴs／Ｒ

　　　∆Ｘi＝－Ｘi－1－（Ｒ²－（Ｙi－１＋∆Ｙi）²）^1/2

　　 Ｘi＝Ｘi－１＋∆Ｘi

Ｙi＝Ｙi－１＋∆Ｙi

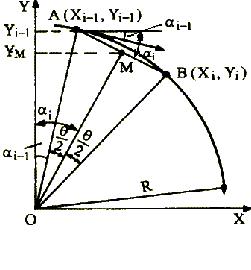
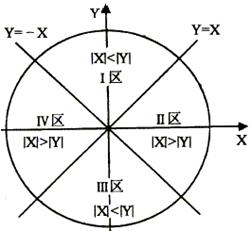
图４-22　弦线法顺圆插补示意图 　　 图4-23　分区图

分区情况见图４－２３。由此，不难得到其流程图４-２４。

弦线法的精度比切线法高。

（3）割线法（二阶ＤＤＡ算法）

一阶算法时曾得到：sinθ＝θ－θ³/3!＋θ⁵/5!－……

　　　 cosθ＝1－θ^２/２!＋θ⁴/４!－……

我们现在取两阶近似，即为二阶ＤＤＡ算法：

　　sinθ＝θ－θ³/3!≈θ

cosθ＝1－θ^２/２!≈１－０.５×θ²

图4-25逆圆第一象限插补时，可计算得到：

　∆Ｘi＝Ｋ×Ｙi－1－０.５×Ｘi－1Ｋ²

∆Ｙi＝－Ｋ×Ｘi－1－０.５×Ｙi－1Ｋ²

Ｘi＝Ｘi－１＋∆Ｘi

Ｙi＝Ｙi－１＋∆Ｙi

按此编制程序流程图4-26。割线法的精度比弦线法高。

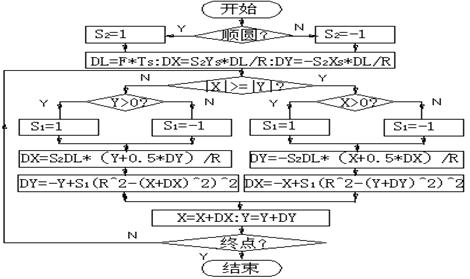
图４-24　弦线法圆弧插补流程图

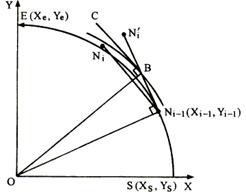
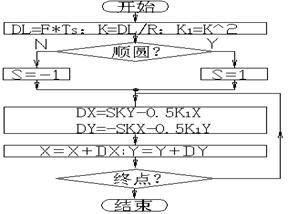
图４-25　割线法逆圆插补示意图 图４-26　割线法圆弧插补流程图

3．参考程序：

直线：

Sub 插补()

Dim l, K, a, B, f1, t

x动点对起