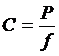一、汽车钢板弹簧的基本特性
钢板弹簧的主要功能是作为汽车悬架系统的弹性元件,此外多片弹簧的片间摩擦又起作系统的阻尼作用,多数钢板弹簧通过卷耳和支座兼有导向作用。但就其基本的受力情况及结构特点,钢板弹簧具有以下两个基本特征:
1、无论钢板弹簧以什么形式装在汽车上,它都是以梁的方式在工作,也就是说它的主要受力方向垂直于钢板弹簧长度。同时,由于受变形相对其长度很小,因此可以利用材料力学中有关小挠度梁的理论,即线性原理来进行分析计算。
2、钢板弹簧装在汽车上所承受的弯矩,基本上是单向载荷,因而其弯曲应力也是单向应力。
二、等应力梁的概念
椭圆形 半椭圆形 四分之一椭圆形
除早期的汽车采用过椭圆形钢板弹簧,近代汽车绝大多数采用半椭圆形钢板弹簧,只有极少数采用四分之一椭圆形钢板弹簧。无论何种形式的钢板弹簧,就其总成而言,都是根部支承,端部承爱集中载荷,它都是以梁的方式在工作。
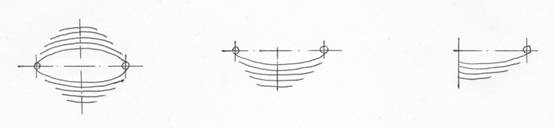
众所周知,理想的梁应该是一根等应力梁,这样才能获得材料的最佳利用。对于钢板弹簧而言,无论单片或多片,设计者应该努力将它设计成等应力梁或近似于等应力梁。
就单片梁而言,当只有单片承爱集中载荷时,有两种轮廓可以满足等应力梁的要求。对于等厚度者,宽度应成三角形,对于等宽度者,厚度为抛物线形状。
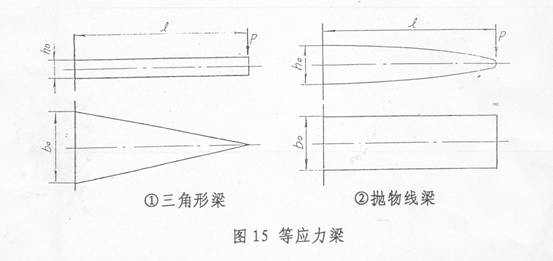
当然,从理论上讲,只要截面系数沿片长方向与弯矩成比例变化,都可以成为等应力梁。然而汽车上几乎没有采用同时变厚又变宽的弹簧。上述轮廓线只是对弯曲应力而言,实际上钢板弹簧端部受剪切强度的要求以及卷耳的存在,第一种轮廓只能是在三角形端部加上等宽的矩形或整个宽度成为梯形,而第二种轮廓只能是抛物线端部接上一段等厚度的矩形或厚度按梯形变化的梁。
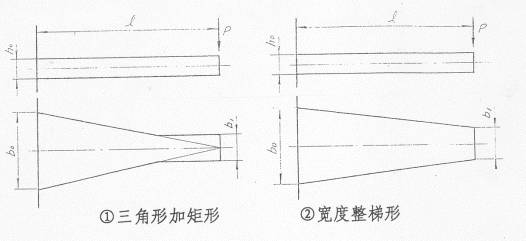
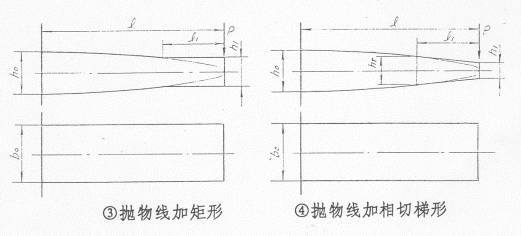
为了简化轧制工艺,对于等宽度者,可用梯形代替抛物线。此外,根部也设计成为平直的,便于与支承座贴合,也就是说,或者由梯形和根部、端部为矩形的三段直线构成。
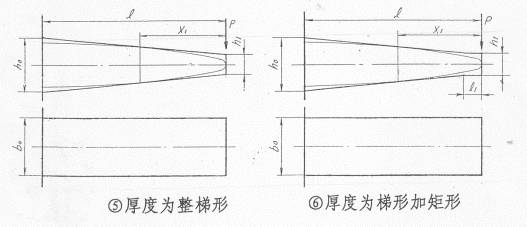
所以,在实际应用上,只能把弹簧设计成为近似的等应力梁。由于结构上的原因,没有人在汽车上采用等厚度变宽度的单片钢板弹簧,但等宽度变厚度的单片钢板弹簧早就得到实际的应用。
三、单片钢板弹簧的计算
1、计算公式:
单片钢板弹簧,就是一根简单的承爱集中载荷的梁,我们可以利用材料力学中分析小挠度梁的方式,寻出计算挠度、刚度、沿长度分布的最大应力以及比应力的公式。当然,梁的轮廓线(断面变化情况)不同,寻出的公式也不同。然而,对它们整理之后,我们可以得到一组形式完全一样的计算公式,仅以形状系数的差异来区别各种不同轮廓线的单片钢板弹簧。
可把普通使用的对称半椭圆钢板弹簧当做简支梁来分析,它的计算公式是:
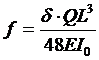 …………(1)
…………(1)
![]() ………(2)
………(2)
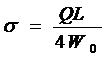 ……(3)
……(3)
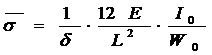 ……(4)
……(4)
式中:f-挠度 c-刚度 σ-根部应力
![]() -比应力(单位变形所产生的应力,反映同样f的情况下应力幅的大小) δ-形状系数, Q-弹簧根部负荷,Q=2P,L-弹簧长度,L=2L,E-弹性模数,I0-根部惯性矩,W0-根部断面系数。
-比应力(单位变形所产生的应力,反映同样f的情况下应力幅的大小) δ-形状系数, Q-弹簧根部负荷,Q=2P,L-弹簧长度,L=2L,E-弹性模数,I0-根部惯性矩,W0-根部断面系数。
2、形状系数
(1)等厚度,宽度为梯形
形状系数由端部与根部之惯性矩比值所确定。
![]() ………(5)
………(5)
而 ![]()
式中:I1-端部惯性矩
I0-根部惯性矩
(2)等宽度,厚度为抛物线加上矩形端部
形状系数取决于矩形段长度与总长之比
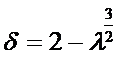 ………..(6)
………..(6)
式中: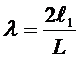
![]() -为矩形段单边长度
-为矩形段单边长度
(3)等宽度,厚度为抛物线和端部及根部为矩形三段组成。
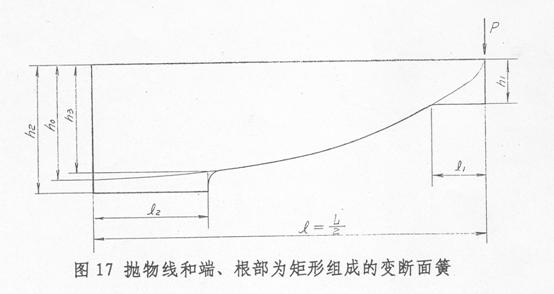
将根部的矩形段延长,并比理论抛物线根部厚度增大一些,是为了减小根部应力,克服这部位由于接触应力和应力集中导致的早期损坏。
对这种单片簧进行分段积分求变形,最后得到的计算公式也具有与上述式(1)….(4)相同形式,但式中之根部惯性矩与断面系数等,均指理论抛物线根部的断面参数,即:
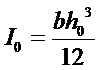
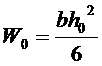
而形状系数:
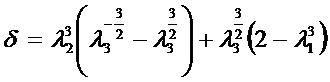 ………..(7)
………..(7)
式中:
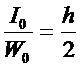
![]()
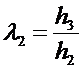
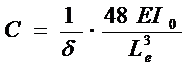
这种弹簧的最大应力不在根部,而在整个抛物线区段,所指比应力也如此。
(4)等宽度,厚度由三段直线组成。
为了使轧制工艺和检验方法简便些,可以将上述抛物线区段用直线代替,形成一根由三段直线组成的变断面梁。
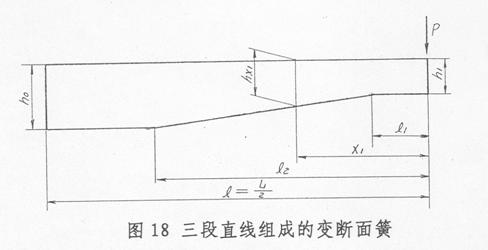
同样,对这种弹簧分段积分求变形,经整理后,其计算公式具有与上述式(1)….(4)相同形式,其形状系数
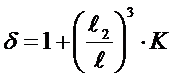 ………..(8)
………..(8)
式中: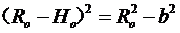
其中 ![]()
![]()
![]()
![]() -为弹簧半长
-为弹簧半长
按上述式(3)、(4)计算的应力和比应力,均是根部的应力和比应力,但不一定是沿片长的最大应力。
从以上公式可以看出,对于理想的等应力梁,若是等厚度的三角形梁, η=0结果δ=1.5,若是等宽度的抛物线梁,λ1=0,λ2=λ3=1,结果δ=2。它们都可以获得最大的形状系数即最大挠度增大系数。对于等宽等厚的矩形梁δ=1为最小值。其它各种轮廓,形状系数都介于这二者之间。
3、确定轮廓线的基本原则
在实际应用上,如前所述,端部必需要有一个矩形段,而根部由于支承座的工艺方便性,也要有一段平直的矩形段,所以实际的变截面弹簧只能是上述两种轮廓。
那么,设计上如何来确定轮廓线呢?
①、从设计的合理性讲,基本的原则是使应力分布尽量均匀,也就是尽量接近等应力分布。这里可以引入材料利用率的概念,也就是在相同的最大应力提前下,采用材料利用率最高的轮廓线。
所谓材料利用率,就是弹簧的单位体积或重量所贮存的弹性能与理想等应力梁的单位体积或重量所贮存的弹性能的比值。
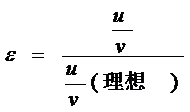
一般多片簧材料利用率ε=60%,变截面簧ε=75%~85%。
②、但在设计时还要根据工艺和成本等因素来决定采用何种轮廓线。即使确定了基本的轮廓线之后,就每一类轮廓而言,也要合理地选择尺寸参数,使它获得最佳的材料利用率,才不会造成不必要的浪费。当然弹簧不仅仅承受弯曲应力,所以还应综合考虑或计算根部接触应力,端部卷耳应力等。有时为了降低接触应力或卷耳应力,就必须牺牲一定的材料利用率。
设计时,除了应力核算外,还要保证所要求的刚度。
四、多片钢板弹簧的刚度和工作应力计算
计算多片钢板弹簧的目的,也就是为了求得它的刚度,比应力以及承载后的挠度、应力等。此外还要计算总成装配后各片的预应力。
多片钢板弹簧的计算,是建筑在一定的假设基础上的。假设不同,计算结果也不同。有两种最典型的,又是截然相反的假设,即共同曲率法和集中载荷法,实际的多片簧,往往不完全符合这两种假设中的某一种,或者在工作过程中介于它们中间变化。
1、共同曲率法:
按此假设,在任何负荷作用下,钢板弹簧所有叶片彼此沿整个片长上无间隙地相接触,这样,在钢板弹簧的任何截面上,相邻的叶片都具有相同的曲率半径。
如果不计各叶片由于厚度形成的曲率半径的差值按此假设,即同一截面的各叶片在任何负荷下都是曲率半径相同。我们如果将多片的钢板弹簧各片从中心线纵向切开,展成平面,组成一个新的单片弹簧,可以看到,这个单片簧的力学特征和做了共同曲率法假定的多片簧完全一样的,这样,就可以利用单片弹簧的计算方法来计算多片簧。所以共同曲率法又称为展开法。
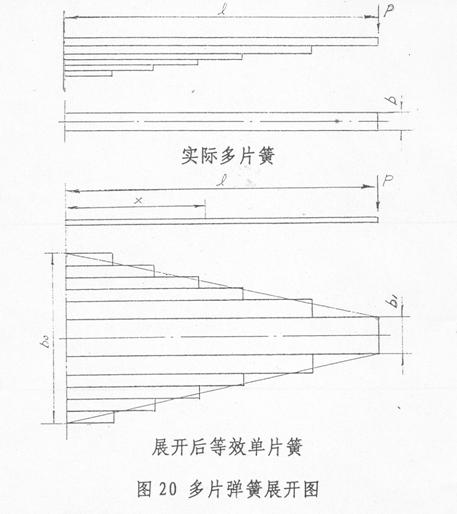
这时,又可以有两种不同的方法来确立这根等效的单片簧。一种是以宽度为梯形状的单片簧来代替多片簧,另一种是保留多片簧各叶片的端部形状,以一种锯齿形(阶梯形状)的单片簧来代替多片簧。
(1)单片梯形梁的假设
将多片钢板弹簧简化为单片梯形梁,可以很容易地得到计算结果。这时只要对展开后的单片簧,将其端部总宽度和根部总宽度的边缘联成一线,就形成一根梯形梁,见上图。利用材料力学小挠度梁的方法,导出的公式(1)、(2)、(3)、(4)、(5)。可以用来计算多片簧。其中根部惯性矩I0。为各片惯性矩之和,端部惯性矩为主片等长的重叠片之和。当各片厚度即惯性矩都相同时
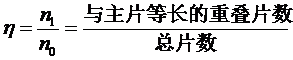
对于各片厚度或惯性矩不同的多片簧,应该按等效即惯性矩相当的方法来确定各片的展开宽度,也就是展开后的各片厚度都彼此相同,但必须保证展开前后各片惯性矩不变,而宽度可以与原片不同。这样按式(3)和(4)计算出的静应力和比应力,只是根部的当量或平均应力、比应力,并不反映各片根部的应力、比应力。
根据共同曲率法的假设,在同一截面上各片曲率半径的变化值相同,则各片所承受的弯矩正比于惯性矩。又根据平衡条件,截面上各片弯矩之和等于外力引起的力矩,可以分别求出各自叶片根部的应力和比应力:
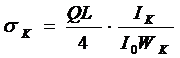 …………(8)
…………(8)
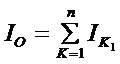 …………(9)
…………(9)
式中:IK-第K片根部惯性矩
WK-第K片的断面系数
还可以求出各叶片应力沿片长的分布:
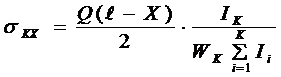 ……..(10)
……..(10)
式中:![]()
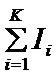 -在x长度处各片惯性矩之和,K为该处的片数。
-在x长度处各片惯性矩之和,K为该处的片数。
IK、WK-在x长度处所计算叶片之惯性矩,断面系数。
(2)单片锯齿形梁的假设(阶梯形)
将多片簧的叶片按等效的原则展开成为等厚的单片簧,而各片端部保留原状,就形成一根边缘为锯齿形或阶梯的梁,对于端部不切角不轧薄的叶片,展开后就成为有规则的垂直锯齿状。见上图,同样,可以利用材料力学求小挠度梁变形的方法,利用分段积分,求得梁的变形即挠度,或改写成刚度公式。
对于对称的半椭圆钢板弹簧:
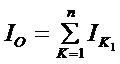 ………….(11)
………….(11)
式中:![]()
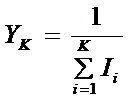
而 ![]() -为主片之半长
-为主片之半长
![]() -为第K片之半长
-为第K片之半长
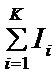 -为从第一片到第K片的惯性矩之和
-为从第一片到第K片的惯性矩之和
![]() - 为修正系数
- 为修正系数
根据我们的经验:
端部切角或轧薄头取 ![]() =0.85~0.87
=0.85~0.87
端部为矩形取 ![]() =0.88~0.92
=0.88~0.92
以上公式称巴希洛夫斯基公式,有的把它称为计算刚度的精确公式,实际上,此公式并不精确,主要原因是它的数学模型中让叶片端部都承受弯曲,即端点的断面惯性矩都有效,这就违反了各叶端点不能承受弯矩的边界条件,所以利用以上公式计算出来的刚度值要比实际测量值大得多,所以就引用了一个经验系数来修正。
对于不对称的半椭圆钢板弹簧:
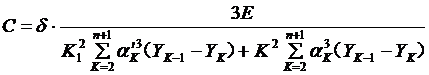 ….(12)
….(12)
式中: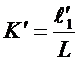
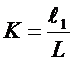
而![]() 、
、![]() 为主片和第K片的另一半长
为主片和第K片的另一半长
2、集中载荷法
与共同曲率法的假设正相反,集中载荷法假设多片簧在任何负荷作用下,各叶片之间只在端点和根部无摩擦地接触,只在这些部位有力的传递。所以,集中载荷法又称端点法。
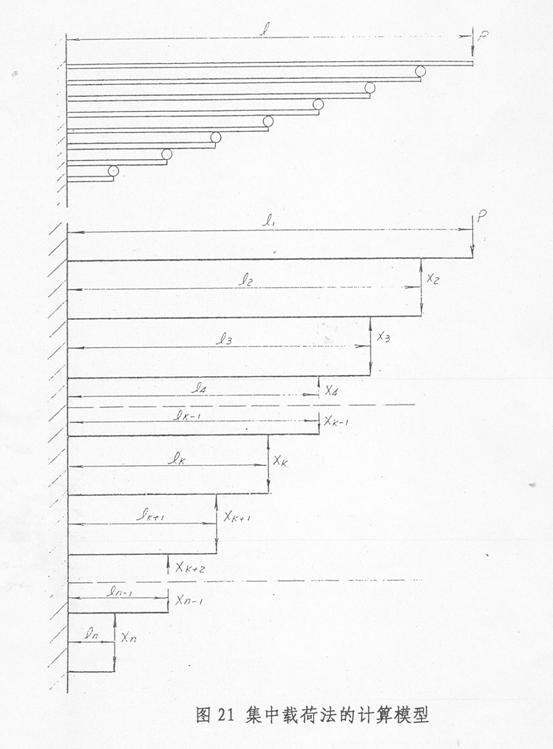
按照这样的假设,多片簧的力学模型如图所示。这里有n-1个未知力X2….Xn,根据材料力学求梁变形的方法,可以对每个单片求其端点以及与下一片端点接触处的变形,然后,根据变形一致原理,令相邻两片在端点接触处的变形相等,即可得到n-1个方程式,经整理后得:
A2P+B2X2+C2X3=0
A3X2+B3X3+C3X4=0
…………
AK XK-1+BKXK+CKXK+1=0
……
An Xn-1+BnXn =0 (13)
式中的系数:
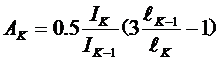
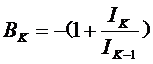
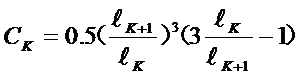
此方程组为n-1元线性方程,用代入法就可以解出X2….Xn。知道了各单片的受力情况,就更容易求出其它的参数了。例如根据第一片承受的力P和X2,可以算出端点也就是弹簧总成的变形,进而折换成刚度:
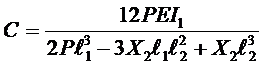 ……….(14)
……….(14)
从式(13)解出X2代入式(14),就得到C位。同样,可求出各单片的应力分布。
根部应力:
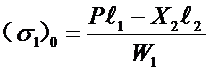
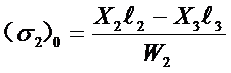
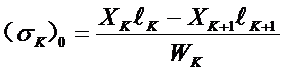
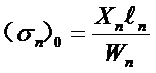
与下一端点接触处的应力:
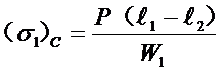
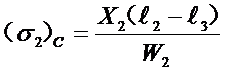
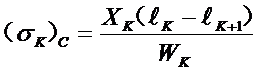
![]()
因为各单片只承受集中载荷,故应力分布呈折线状。知道了这两点的应力值,就知道了沿片长的全部应力值了。
3、多片弹簧各单片长度的确定
在设计多片钢板弹簧时,首先要确定各片长度,才有可能按上述的各种方法来计算刚度和应力。本节所讨论的,是当主片长度确定之后,如何按各片的惯性矩来确定各片的长度。基于上述的两种假设,导出了两种选择长度的方法,展开作图法和集中载荷法,下面主要介绍展开作图法。
展开作图法:
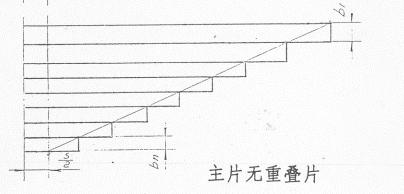
根据上述等效的原则,对于主片无重叠者,可根据等应力梁为三角形轮廓的原则,从U型螺栓跨距之半(下侧边)到主片端点(上侧边)连一直线,此直线与各单片上侧边的交点即为各片长度。
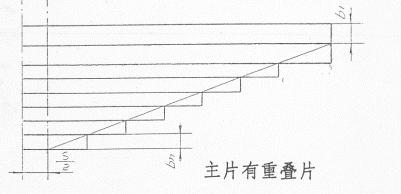
如果存在与主片等长的重叠片,就按梯形轮廓线来确定各片长度,即U型螺栓跨距之半(下侧边)到最后一个重叠片的端点(上侧边)连一直线,此直线与各叶片的上侧边交点即为各片长度。
五、汽车钢板弹簧设计步骤
汽车钢板弹簧设计计算过程,大致可分为三个阶段,第一阶段:钢板弹簧基本参数计算;第二阶段:钢板弹簧装车后的参数验算;第三阶段:钢板弹簧结构设计。
1、钢板弹簧基本参数计算
(1)首先要确定与整车设计相关的基本参数
①、弹簧上的载荷(簧上重量、悬架重量)
簧上重量主要指作用在车轮以上的重量。根据总布置给定的轴荷减去非悬架重量,就是弹簧上的载荷。
非悬架重量是指位于钢板弹簧以下的重量。指车轮、车轴等总成,把车轮与车身联系起来的零件(传动轴、纵拉杆、推力杆)的重量分为两半,一半属于非悬架重量,而另一半属于悬架重量。钢板弹簧的重量,正置装配形式的四分之三属于非悬架重量,平衡悬架钢板弹簧重量的四分之一属于非悬架重量。
②、弹簧长度:(支点距)
弹簧长度涉及到整车的总布置,须与总布置商定,在总布置可能的情况下,增加弹簧长度可以降低比应力,提高板簧的使用寿命,并能获得良好平顺性和操作稳定性。(双方商定或由主机厂负责悬架系统设计的给定)
③、静挠度f静:
弹簧的静挠度是指满载静负荷的弹簧的变形量,它是决定平顺性的基本参数。
根据静挠度,初步可以确定前、后悬架的自由振动频率。静挠度和自由振动频率的关系可由下式表示:
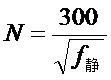
选取较低的自振频率,可以获得良好的平顺性。但是自振频率过低,也就是说静挠度过大,又会出现一些矛盾。
a. 自振频率过低,则弹簧过软,当汽车制动时,便产生严重:“点头”现象,当汽车转弯时,车身侧倾加剧。
b. 静挠度增大后,汽车在坏路面行驶时,就会经常碰撞缓冲块,为了避免经常碰撞缓冲块,则要求相应地增加动挠度,这样就会抬高车架各总成的位置,提高了汽车的重心,并引起汽车在不同载荷下车身高度变化较大。
c. 静挠度和动挠度增加后,车轮的垂直位移增加,使汽车的操作稳定性变坏。
载重汽车在满载时的自振频率和静挠度一般为:
前悬架N=100~125次/分,f静=55~90mm。
后悬架N=105~130次/分,f静=50~80mm。
为了减少汽车行驶过程中产生纵向频簸(纵向角振动),设计悬架时,前、后悬架的自振频率应尽可能接近。一般前、后频率的比值取0.85~1。
④、动挠度
在动载荷作用下,弹簧从静载荷位置起,变形到结构所容许的最大可能变形量。
一般取![]() (载重车)
(载重车)
⑤、满载时弹簧弧高
一般希望当汽车满载时弹簧平直,使弹簧在对称位置下工作,但考虑到弹簧在使用过程中会产生永久变形,所以通常取弧高为10~30mm。
⑥、骑马螺栓中心距
主要用来计算装车状态时的刚度。若骑马螺栓是斜直布置,骑马螺栓中心距取上下的平均值。
(2)钢板弹簧基本参数和尺寸的确定
钢板弹簧总成的刚度,比应力和自由弧高一旦确定,这个钢板弹簧的基本面貌也就确定了。这三个参数只取决于弹簧的尺寸规格,与外负荷的变化无关,故称之谓钢板弹簧的基本参数。
①、刚度的确定
当静挠度确定以后,钢板弹簧期望的刚度C就可以由下式决定。
钢板弹簧设计最理想的是设计成等应力梁材料利用率最高,但实际上由于制造和结构上的原因,钢板弹簧不可能做成等应力梁,而是介于等截面梁和等应力之间,实际钢板弹簧展开面是接近于梯形,因此计算时极近似于梯形多片钢板弹簧的公式。
对于半椭圆式钢板弹簧
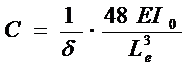
根据期望的刚度C来计算弹簧的几个主要尺寸。
a. 形状系数δ:
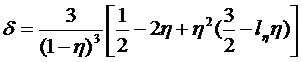
而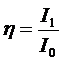 。
。
先确定主片的重叠片数n1,然后估计总片数n。根据两者惯性矩的比值η,在代入上式。或者查表求出形状系数δ。
b. 初定无效长度LS
我们把夹紧部位中的一部份看成不起作用的,称为无效长度。因为夹紧零件不可能是绝对刚性的,所以不可能将骑马螺栓中心距内的全部长度当做无效长度。
一般说,无效长度与骑马螺栓中心距S成正比,但又和下列因素有关。
1、弹簧底座和盖板长度及端部园角。
2、盖板和弹簧之间是否留有间隙。
3、盖板和底座本身的刚性。
4、弹簧和底座盖板之间是否有软垫。
5、骑马螺栓的拉伸刚度,取决于直径和长度。
6、骑马螺栓的拧紧力矩。
这些影响因素无法用数学公式表达,我们只能将无效长度表示为:
![]()
式中α——无效长度系数
α取决于上述的各因素,只能靠试验来确定,从测定夹紧前、后的刚度变化来确定,或参数类似夹紧结构来确定。
α一般小于1,一般情况下取α=0.5。
根据确定的螺马螺栓中心距S,参数类似的结构初定无效长度系数α,根据给定支点距L,按下式计算有效长度。
![]()
c. 总成总的惯性矩I。
对于各片断面相同的弹簧钢板,![]() 其中n为总的片数,I为每片断面惯性矩。
其中n为总的片数,I为每片断面惯性矩。
对于断面不同的钢板弹簧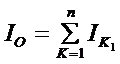 ,其中IK表示各片自己的断面惯性矩,
,其中IK表示各片自己的断面惯性矩,![]() 。
。
对于矩形断面: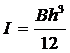
d. 材料的弹性模数E:
对于合金钢一般均可取![]()
②、比应力![]() 的计算
的计算
比应力是单位变形所产生的应力,反映在同样挠度情况下应力幅值的大小,是直接影响钢板弹簧总成疲劳寿命的参数。
对于半椭圆形钢板弹簧:
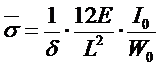
式中总的惯性矩与总的断面系数之比![]() ,对于矩形断面
,对于矩形断面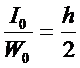 ,即为钢板厚度的一半。
,即为钢板厚度的一半。
建议比应力![]() 值按以下范围选取:
值按以下范围选取:
一般载重车前、后簧![]() =450~550kgf/cm2/cm
=450~550kgf/cm2/cm
越野车平衡悬架簧![]() =650~800kgf/cm2/cm
=650~800kgf/cm2/cm
载重车后悬架付簧![]() =750~800kgf/cm2/cm
=750~800kgf/cm2/cm
如果所得的比应力值不合适,就应修改片厚和片数。修改后应使根部总惯性矩尽量少变化,即刚度无明显改变。最后按修改值再重算一次刚度。
③、总成自由弧高的确定
根据悬架布置要求所确定的满载弧高H。按下式计算无载夹紧弧高H1:
H1=fm+Ho
钢板弹簧总成自由弧高:
![]()
由于骑马螺栓夹紧后,将引起钢板弹簧总成的弧高发生变化,其弧高变化量为![]() ,可以参照已有的类似弹簧的变化量或按下式计算夹紧所引起的弧高变化量
,可以参照已有的类似弹簧的变化量或按下式计算夹紧所引起的弧高变化量![]() 。
。
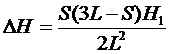
2、钢板弹簧装车后的参数验算。
经过上面的计算,钢板弹簧总成的基本规格(长度、宽度、厚度、片数)和基本参数(刚度、比应力、自由弧高)就确定了。以下就根据所确定的基本参数来核算装车后的状况。
(1)系统的自振频率:
按已知的弹簧负荷P和已选定的夹紧刚度C,先算出该负荷下的静挠度。
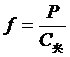
这样就可以算出该负荷下的自振频率
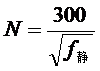 (次/分)
(次/分)
一般要计算满载和空载两种工况。
(2)静应力
按已确定的比应力![]() ,即可算出对应某静挠度f的静应力。
,即可算出对应某静挠度f的静应力。
![]()
片厚不同的单片,比应力不同,因此根部静应力也不同,主要计算满载时的静应力。
对于钢板弹簧表面经喷丸处理后,推荐满载静应力值处在下列范围:
前簧:![]()
后主簧:![]()
后付簧:![]()
平衡弹簧:![]()
由于材料和工艺条件的不断进步,设计所用的许用应力值有逐步提高的趋势。
(3)极限应力
钢板弹簧达到极限动行程的应力值称极限应力。
极限应力由下式计算:
![]()
极限应力的许用值为:
一般弹簧:![]() ≤
≤![]()
平衡弹簧:![]() <
<![]()
极限动行程的大小和汽车的使用条件以及所选用的满载静挠度值fm有关,可用下式表示:
![]()
系数d的范围可取
城市用车辆 d=2~2.5
公路用车辆 d=2~3.5
越野车辆 d>3.5
可见,越柔软的弹簧(fm越大),就应选择较小的比应力![]() ,才能保证弹簧的静强度。
,才能保证弹簧的静强度。
弹簧的软硬不能用C反映,最终要与承载负荷联系在一起。
(4)前簧在最强制动时的强度校核:(纵扭校核)
设计前钢板弹簧时,还必须校核强制动时的强度,以免根部纵扭塑变或卷耳损坏。这对重心较高、轴距较短的汽车,以及长度较短的前簧更为突出。
①、工况的确定:
我国载重汽车的制动系统习惯采用较低同步附着系数,也就是说,在好路面上,都是后轮先抱死。我们从试验结果知道,制动拖印后,轮胎对地面的附着系数约下降20%。从这点出发,我们都按后轮附着系数下降20%来计算。都是把后轮制动力按0.8ф计算,对于前轮,存在三种情况:
a. 前轮压印,未抱死,附着系数全部利用,(最强制动状态)![]() 。
。
b. 前轮拖印,也抱死,附着系数也下降20%,![]() 。
。
c. 前制动器较小,达不到压印程度,这时按制动器的最大力矩来计算。 ![]()
ф=0.7 ф--轮胎对地面的附着系数
ф0=0.4 ф0--同步附着系数
②、计算步骤:
① 前轴转移负荷G1d:
制动时前轴负荷要变大,按平衡条件,列出 ∑X=0. ∑Y=0. ∑M=0.
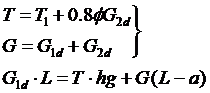
而静止状况时:车的重心:G=G1+G2
G(L-a)=G1L
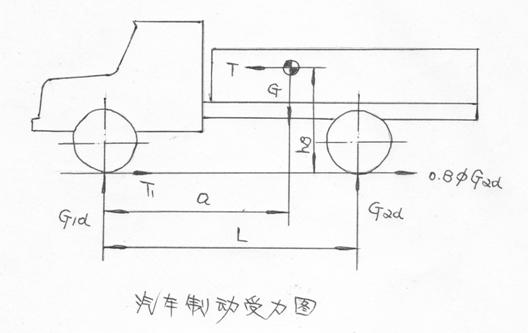
式中:T——重心处的总惯性力 T1——前轮制动力(双边)
G1d——前轴转移后负荷 G2d——后轴转移后负荷
G1 ——前轴静负荷 G2 ——后轴静负荷
L —— 轴距 a ——重心至前轴距离
hg ——重心离地高
前轮压印时:![]()
代入①式导出:
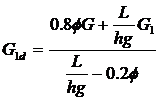
前轮拖印抱死时,![]()
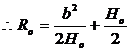
前轮制动力达不到压印时:![]()
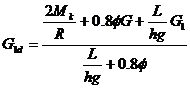
式中: MK —— 前制动器最大制动力矩(单边)
R —— 前轮半径
以上根据具体车型制动器的参数,决定计算何种工况。若第三种工况的T1小于第一种工况,则按第三种工况计算,否则按一、二种工况计算。
b. 轴荷转移后的前簧垂直负荷
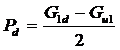
式中:Gu1——前悬架的非簧载重量
G1d——分别被三种Ⅰ况计算
c. 前簧承受的纵扭力矩
将作用在地面的制动力T1对第一片取矩得:
M=0.5T1(R+A1+∑h)
式中:A1——前轮中心至弹簧底面距离
∑h——前簧总厚度
引用三种工况的计算结果,就可以分别算出三种工况下的前簧纵扭力矩。
(4)前簧根部的纵扭平均应力
①、根部取U螺栓全部减掉 Lr=L-S
②、纵扭力矩均匀地分摊到根部的前、后两端。
③、按共同曲率法,只算平均(当量)应力。
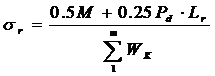
这样计算的结果σr很高。我们认为取φ=0.7,并设定货物重心高于车箱地板300mm来计算整车重心高度hg,这样所得的应力值,如不高于材料的屈服极限σs可认为是安全的。
[σr]≤σs(12500~13000kgf/cm2)
③、前簧卷耳应力
按所求到的前轮制动力T1,来核算卷耳根部应力,它由弯曲应力和拉应力合成,即
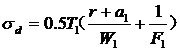
式中:r——耳孔半径
a1——主片中性层至受拉面距离, ![]()
W1——主片断面系数
F1——主片断面积
卷耳的许用应力[σd]<3500kgf/cm2
必要时后簧也要进行制动工况和最大驱动工况的卷耳强度校核。
3、钢板弹簧的结构设计
结构设计的任务:由选型设计已知的规格尺寸及总成弧高,进行具体的零件结构和尺寸的设计,并计算有关的参数。
结构设计的内容:
(1)选择各单片的长度,求各单片的弧高、曲率半径(首先求出总成的曲率半径)。
(2)设计全部零件的结构、尺寸、参数。
(3)完成全部零件的工作图。
(一)、各片长度的确定:
(1)确定长度的目的:尽可能使应力在片间和片长方向的分布合理,使寿命可能的提高。
(2)确定长度的方法:
①展开作图法
②计算法(共同曲率法)
(3)片长的修正
① 主片的修正:
a. 若两端是滑板结构(载重车的付簧、平衡悬架后簧)要增加足够的滑动长度。
b. 有时还将端部制成与主片曲率不同的特殊曲率,以满足主片与滑板接触点的变化要求。
c. 若主片前端是卷耳,后端是滑板结构,那末第二片前端应是包耳结构,后端的第二片或第三片最好要制成弯钩,防止弹簧从滑板支架溜出,弯钩的位置及尺寸取决于反跳限位行程。
d. 主片两端为卷耳结构,为了加强主片和保护卷耳,第二片前端常采用包耳结构,以防止卷耳折断后发生事故,第二片后端有时采用包1/4。
② 夹子片的修正:当总成作用长度比较小,片数较多时,可能出现夹子布置位置比较小,有干涉现象,这是长度应进行适当调整。
修正方法:a. 夹子片长度增加,夹子片下一片的长度减小。
b. 缩短铆钉孔至端部的距离(最小20mm)。
c. 控制公差。
③ 从应力测定或使用中发现应力分布不均匀,在使用中经常某片某处断裂,可适当的修正长度以调整应力分布。
(4)片端形状的确定:
在确定片长的同时,应根据要求,考虑片端所采用的形状。
①、端部为矩形:制造简单,在载重汽车上广泛使用。但是,这种簧片因压力集中,将引起各片应力分布不均,因而增加了它们之间的摩擦和磨损。并有噪音,另外,也增加了自重。
②、端部为梯形:与等应力梁较为近似,在某种程度上克服了矩形端的缺点,重量轻、端部接触比较柔和、摩擦磨损比较小、应力分布有所改善、噪音比矩形小。但在制造上增加了一边剪切工序,在载重汽车上也使用得较多。
③、端部轧扁成斜锥(或加衬垫):是按等应力梁的原则压延其端部而得到必要的变截面形状。这样改善了应力分布情况,增加了片间的弹性,减少了片间的摩擦,降低了噪音,也减轻了自重,目前在我厂已较为广泛的采用。
(二)各片工作应力的计算:
(1)计算各片工作应力的目的:
① 检查片长的设计合理性。计算结果与应力测定进行比较。
② 为选取各单片,装配后的预应力σok提供参考尺度。
(2)各片工作应力的计算方法:
① 集中载荷法:
如果是为了选取预应力,采用此种方法比较合适,因短片的根部应力往往比较高,而用集中载荷法确定的各片σk,短片符合实际的情况。
② 共同曲率法:
如果是为了与应力测定值比较,进而评价弹簧的设计,不妨同时用集中载荷法与共同曲率法进行计算比较。
(三)各单片弧高的确定:
(1)确定的原则:
① 各单片装配成总成后,选取合适的预应力σok,以达到较高的使用寿命。
② 各单片组装成总成后,总成的自由弧高H。符合选型设计的要求。
(2)确定的方法:
① 由给定的总成自由弧高Ho,长度L确定总成曲率半径R。
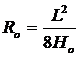
②确定各单片组装成总成后的预应力σok。
③根据求出R。、σok确定各单片的自由弧高hK。
(四)确定总成自由状态的曲率半径R。:
(1)总成为两端都是卷耳结构的
已知:总成自由弧高δo(计入卷耳半径),第一片的伸直长度L卷耳孔半径r。
方法:
H。(不计卷耳半径)=δo(计入卷耳半径)-r
![]()
(2)总成两端都是滑板结构(假定为整圆弧)
已知:总成的自由弧高H。
总成作用弦长Lo,Lo=2b
方法:![]() (勾股弦定理)
(勾股弦定理)
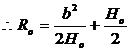
(3)前端为卷耳,后端为滑板。
已知:总成自由弧高δo(计入卷耳半径)
总成作用弦长Lo,Lo=2b 卷耳半径r
方法:![]() (不计入卷耳半径)-
(不计入卷耳半径)-![]()
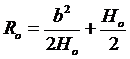
(五)确定各片预应力的分配
(1)确定各片预应力的目的:
① 总成中片厚不等,往往主片厚度大于小片(短片)厚度。
这时:![]() 长片(主片)>
长片(主片)>![]() (短片)
(短片)
那么:σ长片>σ短片
结果:长片的寿命<短片的寿命
因此就采用施加预应力的办法。
σok长片![]() +σ长片工作应力=σ合成应力
+σ长片工作应力=σ合成应力
σok短片![]() +σ短片工作应力=σ合成应力
+σ短片工作应力=σ合成应力
满足自平衡条件:
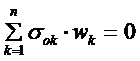
② 总成各片厚度相同
![]() 长片=
长片=![]() (短片)
(短片)
又因:主片、长片受力复杂,制动时、起步、侧滑时都有一个附加力。
![]() 主片寿命<短片寿命
主片寿命<短片寿命
因此:σok 主片取负值 σok 短片取正值
满足自平衡条件:
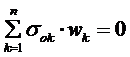
最后保证:长片寿命>短片寿命
为什么要要求主片寿命>短片寿命
[1] 主片、长片成本高
[2] 主片受力复杂、易断、易发生事故
③ 使单片装入总成后,片间贴合良好,易保证在任何工作条件下,各片都参加工作。片间、片长应力分布均匀。
(2)确定各片预应力的方法:
用集中载荷法(列表计算)得到各片的根部力σ根k,作为比较尺度。
① 第1~4片预应力为负值,其绝对值![]() 是递减的。
是递减的。
② 第5~最末片二片预应力为正值,绝对值![]() 是递增的最末二片要减一些。
是递增的最末二片要减一些。
③ 主片σ根主+σok主≈3000kg/cm2左右,末片σmax+σok
<7500~8000kgf/ cm2。
满足自平衡条件:
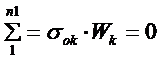
六、各单片在自由状态下曲率半径Rk和弧高hk的计算
利用材料力学的公式:
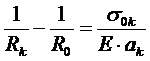
式中:Rk——各单片在自由状态下的曲率半径
R0——总成曲率半径
ak——断面中性层到受拉面的距离
各片的弧高:
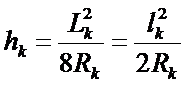
1;所有标注为智造资料网zl.fbzzw.cn的内容均为本站所有,版权均属本站所有,若您需要引用、转载,必须注明来源及原文链接即可,如涉及大面积转载,请来信告知,获取《授权协议》。
2;本网站图片,文字之类版权申明,因为网站可以由注册用户自行上传图片或文字,本网站无法鉴别所上传图片或文字的知识版权,如果侵犯,请及时通知我们,本网站将在第一时间及时删除,相关侵权责任均由相应上传用户自行承担。
内容投诉
智造资料网打造智能制造3D图纸下载,在线视频,软件下载,在线问答综合平台 » 汽车钢板弹簧的设计(图文教程)